A box contains 3 marbles: 1 red, 1 green, and 1 blue. Consider an experiment that consists of taking 1 marble from the box and then replacing it in the box and drawing a second marble from the box. Describe the sample space. Repeat when the second marble is drawn without replacing the first marble.
(a) S = {(r,r), (r, g), (r,b), (g, r), (g, g), (g, b), (b, r), (b, g), (b, b)}
(b) S = {(r, g), (r, b), (g, r), (g, b), (b, r), (b, g)}
In an experiment, die is rolled continually until a 6 appears, at which point the experiment stops. What is the sample space of this experiment? Let En denote the event that n rolls are necessary to complete the experiment. What points of the sample spare are contained in En? What is (inf(U) 1 En)?
S = {(n, x 1 , …, x n−1 ), n ≥ 1, x i ≠ 6, i = 1, …, n − 1}, with the interpretation that the outcome is (n, x 1 , …, x n−1 ) if the first 6 appears on roll n, and x i appears on roll, i, i = 1, …, n − 1. The event c n n E ) ( 1 ∞ = ∪ is the event that 6 never appears.
Two dice are thrown. Let E be the event that the sum of the dice is odd, let F be the event that at least one of the dice lands on 1, and let G be the event that the sum is 5. Describe the events EF, E ∪ F, FG, EF^c, and EFG.
EF = {(1, 2), (1, 4), (1, 6), (2, 1), (4, 1), (6, 1)}.
E ∪ F
occurs if the sum is odd or if at least one of the dice lands on 1. FG
= {(1, 4), (4, 1)}.
EF c is the event that neither of the dice
lands on 1 and the sum is odd. EFG = FG.
A, B, and C take turns flipping a coin. The first one
to get a
head wins. The sample space of this exper-iment can be defined
by
S = {1, 01, 001, 0001, . . . , 0000 · · ·
(a) Interpret the sample space.
(b) Define the following events
in terms of S:
(i) A wins = A.
(ii) B wins = B.
(iii) (
A ∪ B ) c
.
Assume that A flips first, then B, then
C,
then A, and so on.
A = {1,0001,0000001, …} B = {01, 00001, 00000001, …}
(A ∪ B) c
= {00000 …, 001, 000001, …}
A system is comprised of 5 components, each of which is either working or failed. Consider an experiment that consists of observing the status of each component, and let the outcome of the exper-iment be given by the vector ( x1, x2, x3, x4, x5 ) , where xi is equal to 1 if component i is working and is equal to 0 if component i is failed.
(a) How many outcomes are in the sample space of this
experiment?
(b) Suppose that the system will work if compo-nents
1 and 2 are both working, or if compo-nents 3 and 4 are both working,
or if compo-nents 1, 3, and 5 are all working. Let W be the event that
the system will work. Specify all the outcomes in W.
(c) Let A be
the event that components 4 and 5 are both failed. How many outcomes
are con-tained in the event A?
(d) Write out all the outcomes in
the event AW.
(a) 25 = 32
(b) W = {(1, 1, 1, 1, 1), (1, 1, 1, 1,
0), (1, 1, 1, 0, 1), (1, 1, 0, 1, 1), (1, 1, 1, 0, 0), (1, 1, 0, 1, 0)
(1, 1, 0, 0, 1), (1, 1, 0, 0, 0), (1, 0, 1, 1, 1), (0, 1, 1, 1, 1),
(1, 0, 1, 1, 0), (0, 1, 1, 1, 0), (0, 0, 1, 1, 1) (0, 0, 1, 1, 0), (1,
0, 1, 0, 1)}
(c) 8
(d) AW = {(1, 1, 1, 0, 0), (1, 1, 0,
0, 0)}
A hospital administrator codes incoming patients suffering gunshot wounds according to whether they have insurance (coding 1 if they do and 0 if they do not) and according to their condition, which is rated as good (g), fair (f), or serious (s). Consider an experiment that consists of the coding of such a patient.
(a) Give the sample space of this experiment.
(b) Let A be the
event that the patient is in serious
condition. Specify the
outcomes in A.
(c) Let B be the event that the patient is
unin-sured. Specify the outcomes in B.
(d) Give all the outcomes
in the event B
c ∪ A.
(a) S = {(1, g), (0, g), (1, f), (0, f), (1, s), (0, s)}
(b) A
= {(1, s), (0, s)}
(c) B = {(0, g), (0, f), (0, s)}
(d)
{(1, s), (0, s), (1, g), (1, f)}
Consider an experiment that consists of determin-ing the type of
job—either blue-collar or white-collar—and the political
affiliation—Republican,
Democratic, or Independent—of the 15
members of an adult soccer team. How many outcomes are
(a) in the
sample space?
(b) in the event that at least one of the team
mem-bers is a blue-collar worker?(c) in the event that none of the
team members considers himself or herself an Independent?
(a) 6 15
(b) 6 15 − 3 15
(c) 4 15
Suppose that A and B are mutually exclusive events for which P (A) =
. 3 and P (B) = . 5. What is the probability that
(a) either A or
B occurs?
(b) A occurs but B does not?
(c) both A and B occur?
(a) .8
(b) .3
(c) 0
A retail establishment accepts either the American Express or the VISA credit card. A total of 24 per-cent of its customers carry an American Express card, 61 percent carry a VISA card, and 11 per-cent carry both cards. What percentage of its cus-tomers carry a credit card that the establishment will accept?
Choose a customer at random. Let A denote the event that this
customer carries an American Express card and V the event that he or
she carries a VISA card.
P(A ∪ V) = P(A) + P(V) − P(AV)
= .24 + .61 − .11 = .74.
Therefore, 74 percent of the
establishment’s customers carry at least one of the two types of
credit cards that it accepts.
Sixty percent of the students at a certain school wear neither a ring
nor a necklace. Twenty per-cent wear a ring and 30 percent wear a
necklace. If one of the students is chosen randomly, what is the
probability that this student is wearing
(a) a ring or a
necklace?
(b) a ring and a necklace?
Let R and N denote the events, respectively, that the student wears a ring and wears a necklace.
(a) P(R ∪ N) = 1 − .6 = .4
(b) .4 = P(R ∪ N) = P(R) +
P(N) − P(RN) = .2 + .3 − P(RN)
Thus, P(RN) = .1
A total of 28 percent of American males smoke cigarettes, 7 percent
smoke cigars, and 5 percent
smoke both cigars and
cigarettes.
(a) What percentage of males smokes neither cigars
nor cigarettes?
(b) What percentage smokes cigars but not cigarettes?
Let A be the event that a randomly chosen person is a cigarette
smoker and let B be the event that she or he is a cigar smoker.
(a) 1 − P(A ∪ B) = 1 − (.07 + .28 − .05) = .7. Hence, 70
percent smoke neither.
(b) P(A c B) = P(B) − P(AB) = .07
− .05 = .02. Hence, 2 percent smoke cigars but not cigarettes.
An elementary school is offering 3 language classes: one in Spanish, one in French, and one in German. The classes are open to any of the 100 students in the school. There are 28 students in the Spanish class, 26 in the French class, and 16 in the German class. There are 12 students that are in both Spanish and French, 4 that are in both Span-ish and German, and 6 that are in both French and German. In addition, there are 2 students taking all 3 classes.
(a) If a student is chosen randomly, what is the probability that he
or she is not in any of the language classes?
(b) If a student is
chosen randomly, what is the probability that he or she is taking
exactly one language class?
(c) If 2 students are chosen
randomly, what is the probability that at least 1 is taking a language class?
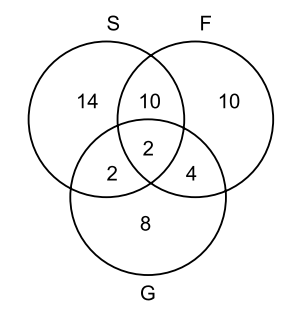
(a) P(S ∪ F ∪ G) = (28 + 26 + 16 − 12 − 4 − 6 + 2)/100 = 1/2
The desired probability is 1 − 1/2 = 1/2.
(b) Use the
Venn diagram below to obtain the answer 32/100.
(attached image)
(c) since 50 students are not taking any of the courses, the probability that neither one is taking a course is (50 2)/ (100 2) = 49/198 and so the probability that at least one is taking a course is 149/198.
A certain town with a population of 100,000 has
3 newspapers: I,
II, and III. The proportions of
townspeople who read these papers
are as follows:
I: 10 percent I and II: 8 percent I and II
and
III: 1 percent
II: 30 percent I and III: 2
percent
III: 5 percent II and III: 4 percent
(The list tells us, for instance, that 8000 people read newspapers I
and II.)
(a) Find the number of people who read only one
newspaper.
(b) How many people read at least two
newspapers?
(c) If I and III are morning papers and II is an
evening paper, how many people read at least one morning paper plus an
evening paper?
(d) How many people do not read any
newspapers?
(e) How many people read only one morning paper and
one evening paper?
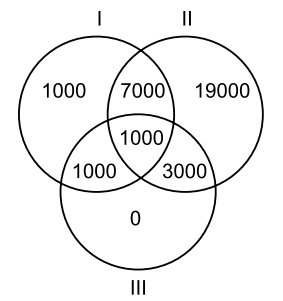
(a) 20,000
(b) 12,000
(c) 11,000
(d) 68,000
(e) 10,000
The following data were given in a study of a group of 1000 subscribers to a certain magazine: In ref-erence to job, marital status, and education, there were 312 professionals, 470 married persons, 525 college graduates, 42 professional college gradu-ates, 147 married college graduates, 86 married professionals, and 25 married professional college graduates. Show that the numbers reported in the study must be incorrect.
Hint: Let M, W, and G denote, respectively, the set of
professionals, married persons, and college graduates. Assume that one
of the 1000 persons is chosen at random, and use Proposition 4.4 to
show that if the given numbers are correct, then
P ( M ∪ W ∪ G )
> 1.
P(M) + P(W) + P(G) − P(MW) − P(MG) − P(WG) + P(MWG) = .312 + .470 + .525 − .086 − .042 − .147 + .025 = 1.057
If it is assumed that all (52 c 5) poker hands are equally likely, what is the probability of being dealt
(a) a flush? (A hand is said to be a flush if all 5 cards are of the
same suit.)
(b) one pair? (This occurs when the cards have
denominations a, a, b, c, d, where a, b, c, and d are all
distinct.)
(c) two pairs? (This occurs when the cards have
denominations a, a, b, b, c, where a, b, and c are all
distinct.)
(d) three of a kind? (This occurs when the cards have
denominations a, a, a, b, c, where a, b, and c are all
distinct.)
(e) four of a kind? (This occurs when the cards have
denominations a, a, a, a, b.)
(a) 4*(13 c 5)/(52 c 5)
(b) 13*(4 c 2)*(12 c 3)*(4 c 1)(4 c 1)*(4 c 1)/(52 c 5)
(c) (13 c 2)*(4 c 2)*(4 c 2)(44 c 1)/(52 c 5)
(d) 13*(4 c 3)*(12 c 2)*(4 c 1)*(4 c 1)/(52 c 5)
(e) 13*(4 c 4)*(48 c 1)/(52 c 5)
Poker dice is played by simultaneously rolling 5 dice. Show that
(a) P { no two alike } = . 0926;
(b) P { one pair } = .
4630;
(c) P { two pair } = . 2315;
(d) P { three alike } = .
1543;
(e) P { full house } = . 0386;
(f) P { four alike } =
. 0193;
(g) P { five alike } = . 0008.
(a) 6*5*4*3*2/6^5
(b) 6*(5 c 2)5*4*3/6^5
(c) (6 c 2)*4*(5 c 2)*(3 c 2)/6^5
(d) 6*5*4(5 c 3)/21
(e) 6*5(5 c 3)/6^5
(f) 6*5*(5 c 4)/6^5
If 8 rooks (castles) are randomly placed on a
chessboard,
compute the probability that none of
the rooks can capture any of
the others. That is, compute the probability that no row or file
con-tains more than one rook.
∏8 i=1 i^2/64*63**68
Two cards are randomly selected from an ordinary playing deck. What is the probability that they form a blackjack? That is, what is the probability that one of the cards is an ace and the other one is either a ten, a jack, a queen, or a king?
2*4*16/52*51
Two symmetric dice have both had two of their sides painted red, two painted black, one painted yellow, and the other painted white. When this pair of dice is rolled, what is the probability that both dice land with the same color face up?
4/36 + 4/36 +1/36 + 1/36 = 5/18
Suppose that you are playing blackjack against a dealer. In a freshly
shuffled deck, what is the prob-ability that neither you nor the dealer
is dealt a
blackjack?
Let A be the event that you are dealt blackjack and let B be the
event that the dealer is dealt
blackjack. Then,
P(A ∪ B) = P(A) + P(B) − P(AB) = 4*4*16/52*51 +
4*4*16*3*15/52*51*50*49 = 0.0983
where the preceding used that P(A) = P(B) = 2 × 4*16/52*51. Hence, the probability that neither is dealt blackjack is .9017.
A small community organization consists of 20 families, of which 4
have one child, 8 have two chil-dren, 5 have three children, 2 have
four children, and 1 has five children.
(a) If one of these
families is chosen at random, what is the probability it has i
children, i = 1, 2, 3, 4, 5?
(b) If one of the children is
randomly chosen, what is the probability that child comes from a
family having i children, i = 1, 2, 3, 4, 5?
(a) p1 = 4/20, p2 = 8/20, p3 = 5/20, p4 = 2/20, p5 = 1/20
(b) There are a total of 4 ⋅ 1 + 8 ⋅ 2 + 5 ⋅ 3 + 2 ⋅ 4 + 1 ⋅ 5
= 48 children. Hence,
q1 = 4/48, q2 = 16/48, q3 = 15/48,
q4 = 8/48, q5 = 5/48
Consider the following technique for shuffling a deck of n cards: For
any initial ordering of the cards, go through the deck one card at a
time and at each card, flip a fair coin. If the coin comes up heads,
then leave the card where it is; if the
coin comes up tails, then
move that card to the end of the deck. After the coin has been flipped
n times, say that one round has been completed. For instance, if n = 4
and the initial ordering is 1, 2, 3, 4, then if the successive flips
result in the outcome h, t, t, h, then the ordering at the end of the
round is 1, 4, 2, 3. Assuming that all possible outcomes of the
sequence of n coin flips are equally likely, what is the probability
that the ordering after one round is the same as the initial ordering?
The ordering will be unchanged if for some k, 0 ≤ k ≤ n, the first k
coin tosses land heads and
the last n − k land tails. Hence, the
desired probability is (n + 1/2^n)
A pair of fair dice is rolled. What is the probabil-ity that the second die lands on a higher value than does the first?
The answer is 5/12, which can be seen as follows:
1 =
P{first higher} + P{second higher} + p{same}
= 2P{second
higher} + p{same}
= 2P{second higher} + 1/6
Another way of solving is to list all the outcomes for which the
second is higher. There is 1
outcome when the second die lands
on two, 2 when it lands on three, 3 when it lands on four,
4
when it lands on five, and 5 when it lands on six. Hence, the
probability is
(1 + 2 + 3 + 4 + 5)/36 = 5/12.
25. A pair of dice is rolled until a sum of either 5 or 7 appears.
Find the probability that a 5 occurs first.
Hint: Let En denote
the event that a 5 occurs on the nth roll and no 5 or 7 occurs on the
first n − 1 rolls. Compute P ( En ) and argue that q n = 1
P ( En
) is the desired probability.
P(En)= (26/36)^n-186/36, ∑inf n=1, P(En) = 2/5
27. An urn contains 3 red and 7 black balls. Players A and B withdraw balls from the urn consecutively until a red ball is selected. Find the probability that A selects the red ball. (A draws the first ball, then B, and so on. There is no replacement of the balls drawn.)
P(A) = 3*9!+7*6*3*7!+7*6*5*4*3*5!+7*6*5*4*3*2*3*3!/10!
An urn contains 5 red, 6 blue, and 8 green balls. If a set of 3 balls
is randomly selected, what is the probability that each of the balls
will be (a) of the
same color? (b) of different colors? Repeat
under the assumption that whenever a ball is selected, its color is
noted and it is then replaced in the urn before the next selection.
This is known as sam-pling with replacement.
P{same} = (5 c 3) + (6 c 3) + (8 c 3)/(19 c 3)
P{different} = (5 c 1)*(6 c 1)*(8 c 1)/(19 c 3)
If sampling is with replacement
P {same} = 5^3+6^3+8^3/(19)^3
P{different} = P(RBG) + P{BRG) + P(RGB) + … + P(GBR) = 6*5*6*8/(19)^3
An urn contains n white and m black balls, where n and m are positive
numbers.
(a) If two balls are randomly withdrawn, what is the
probability that they are the same color?
(b) If a ball is
randomly withdrawn and then replaced before the second one is drawn,
what is the probability that the withdrawn balls are the same
color?
(c) Show that the probability in part (b) is always larger
than the one in part (a).
incomplete
The chess clubs of two schools consist of, respec-tively, 8 and 9
players. Four members from each club are randomly chosen to
participate in a con-test between the two schools. The chosen play-ers
from one team are then randomly paired withthose from the other team,
and each pairing plays
a game of chess. Suppose that Rebecca and
her sis-ter Elise are on the chess clubs at different
schools.
What is the probability that
(a) Rebecca and Elise
will be paired?
(b) Rebecca and Elise will be chosen to represent
their schools but will not play each other?
(c) either Rebecca or
Elise will be chosen to represent her school?
(a) 4/8*4/9*1/4=1/18
(b) 4/8*4/9*3/4= 1/6
(c)P(RUE) = P(R) + P(E) - p(RE) = 4/8+ 4/9-(4/8*4/9) = 13/18
A 3-person basketball team consists of a guard, a forward, and a
center.
(a) If a person is chosen at random from each of three
different such teams, what is the proba-bility of selecting a complete
team?
(b) What is the probability that all 3 players selected
play the same position?
(a) 6/27= 2/9 = 0.222
(b) 2/27 = 1/9 = 0.111
A group of individuals containing b boys and g
girls is lined up
in random order; that is, each of
the (b + g)! permutations is
assumed to be equally
likely. What is the probability that the
person in
the ith position, 1<= i<= b + g, is a girl?
g(b+g-1)!/(b+g)!= g/b+g
A forest contains 20 elk, of which 5 are captured, tagged, and then released. A certain time later, 4 of the 20 elk are captured. What is the probability that 2 of these 4 have been tagged? What assump-tions are you making?
(5 c 2)*(15 c 2)/(20 c 4)= 70/323
The second Earl of Yarborough is reported to have bet at odds of 1000 to 1 that a bridge hand of 13 cards would contain at least one card that is ten or higher. (By ten or higher we mean that a card is either a ten, a jack, a queen, a king, or an ace.) Nowadays, we call a hand that has no cards higher than 9 a Yarborough. What is the proba-bility that a randomly selected bridge hand is a Yarborough?
(32 c 13)/(52 13)
Seven balls are randomly withdrawn from an urn that contains 12 red,
16 blue, and 18 green balls.
Find the probability that
(a) 3
red, 2 blue, and 2 green balls are withdrawn;
(b) at least 2 red
balls are withdrawn;
(c) all withdrawn balls are the same
color;
(d) either exactly 3 red balls or exactly 3 blue balls are withdrawn.
(a) p = (12 c 3)*(16 c 2)*(18 c 2)/(12+16+18 c 7)
(b) 1 - {(16+18 c 7)/(12+16+18 c 7) + (12 c 1)*(16+18 c 6)/(12+16+18 c 7)}
(c) p = (12 c 7) + (16 c 7) + (18 c 7)/(12+16+18 c 7)
(d) p = (3 red for any color) + (3 blue for any other color) - (3 red and 3 blue and any other color)
p = (12 c 3)*(16+18 c 4)+(16 c 3)*(12+18 c 4)-(12 c 3)*(16 c 3)*(18 c 1)/(12+16+18 c 7)
Two cards are chosen at random from a deck of 52 playing cards. What
is the probability that they
(a) are both aces?
(b) have the
same value?
(a) (4 c 2)/(52 c 2) = .0045
(b) 13*(4 c 2)/(52 c 2) = 1/17 = 0.588
An instructor gives her class a set of 10 problems with the
information that the final exam will con-sist of a random selection of
5 of them. If a student has figured out how to do 7 of the problems,
what is the probability that he or she will answer correctly
(a)
all 5 problems?
(b) at least 4 of the problems?
(a) (7 c 5)/(10 c 5) = 1/12 = .0833
(b) (7 c 4)*(3 c 1)/(10 c 5) + 1/12 = 1/2
There are n socks, 3 of which are red, in a drawer. What is the value of n if, when 2 of the socks are chosen randomly, the probability that they are both red is 1/2?
1/2 = (3 c 2)/(n c 2) or n(n-1) = 12 or n = 4
There are 5 hotels in a certain town. If 3 people check into hotels in a day, what is the probability that they each check into a different hotel? What assumptions are you making?
5*4*3/5*5*5 = 12/25
A town contains 4 people who repair televisions.
If 4 sets break
down, what is the probability that exactly i of the repairers are
called? Solve the problem for i = 1, 2, 3, 4. What assumptions are you making?
P{1} = 4/44 = 1/64
P{2} = (4 c 2)[4+(4 c 2)+4]/4^4= 84/256
P{3} = (4 c 3)*(3 c 1)*4!/2!/4^4=36/64
P{4}=4!/4^4=6/64
If a die is rolled 4 times, what is the probability that
6 comes
up at least once?
1-5^4/6^4
Two dice are thrown n times in succession. Com-pute the probability
that double 6 appears at least once. How large need n be to make this
probability
at least 1/2?
1-(35/36)^n
(a) If N people, including A and B, are randomly arranged in a line,
what is the probability that A and B are next to each other?
(b)
What would the probability be if the people were randomly arranged in
a circle?
(a) 2(n-1)(n-2)/n!=2/n in a line
(b) 2n(n-2)!/n! = 2/n-1 if in a circle, n >= 2
Five people, designated as A, B, C, D, E, are arranged in linear
order. Assuming that each pos-sible order is equally likely, what is
the probability that
(a) there is exactly one person between A
and B?
(b) there are exactly two people between A and B?
(c)
there are three people between A and B?
(a) If A is first, then A can be in any one of 3 places and B’s place
is determined, and the others can be arranged in any of 3! ways. As a
similar result is true, when B is first, we see that the probability
in this case is 2 ⋅ 3 ⋅ 3!/5! = 3/10
(b) 2 ⋅ 2 ⋅ 3!/5! =
1/5
(c) 2 ⋅ 3!/5! = 1/10
A woman has n keys, of which one will open her door.
(a) If she
tries the keys at random, discarding
those that do not work, what
is the probability that she will open the door on her kth
try?
(b) What if she does not discard previously tried keys?
(a) P = n-1/n ***n-(k-1)/n-(k-2) *** 1/n-(k-1) = 1/n
(b) P (n-/n1)^k-1*1/n
How many people have to be in a room in order
that the
probability that at least two of them cele-brate their birthday in the
same month is at least 1/2? Assume that all possible monthly outcomes
are equally likely.
If n in the room, P {all different} = 12*11****(13-n)/12*12*12*12
When n = 5 this falls below 1/2. (Its value when n = 5 is .3819)
If there are 12 strangers in a room, what is the probability that no two of them celebrate their birthday in the same month?
12!/(12)^12
Given 20 people, what is the probability that, among the 12 months in the year, there are 4 months containing exactly 2 birthdays and 4 containing exactly 3 birthdays?
(12 c 4)*(8 c 4) * (20)!/(3!)^4(2!)^4/(12)^20
A group of 6 men and 6 women is randomly divided into 2 groups of size 6 each. What is the probability that both groups will have the same number of men?
(6 c 3)*(6 c 3)/(12 c 6)
In a hand of bridge, find the probability that you
have 5 spades
and your partner has the remaining 8.
(13 c 5)*(39 c 8)(8 c 8)(31 c 5)/(52 c 13)*(39 c 13)
Suppose that n balls are randomly distributed into N compartments. Find the probability that m balls will fall into the first compartment. Assume that all N^n arrangements are equally likely.
(n c m)(n-1)^(n-m)/N^n
A closet contains 10 pairs of shoes. If 8 shoes
are randomly
selected, what is the probability that there will be
(a) no
complete pair?
(b) exactly 1 complete pair?
(a) 20*18*16*14*12*10*8*6/20...13
(b) (10 c 1)(9 6)*(8!/2!)*2^6/20*19*18*17*16*15*14*13
If 4 married couples are arranged in a row, find the probability that no husband sits next to his wife.
P(U^4 i=1 Ai) = 4*(2*7!/8!)-6*(2^2*6!/8!)+4*(2^3*5!)/8!-(2^4*4!/8!)
Compute the probability that a bridge hand is void in at least one suit. Note that the answer is not
P(SUHUDUC) = P(S) + P(H) + P(D) + P(C) - P(SH) - ... - P(SHDC) = 4(39 c 13)/(52 c 13) - 6(26 c 13)/52 c 13 + 4(13 c 13)/(52 c 13) = 4(39 c 13) - 6(26 c 13) + 4/(52 c 13)
55 Compute the probability that a hand of 13 cards contains
(a) the ace and king of at least one suit;
(b) all 4 of at least 1 of the 13 denominations.
(a) 4(2 c 2)/(52 c 13)-6(2 c 2)(2 c 2)(48 c 9)/(52 c 13) + 4(2 c 2)^3(46 c 7)/(52 c 13) - (2 c 2)^4*(44 c 5)/(52 c 13) = 4(50 c 11) - 6(48 c 9) + 4(46 c 7) - (44 c 5)/(52 c 13)
(b) P(1 U 2 U...U 13) = 13(48 c 9)/(52 c 13) - (13 c 2)(44 c 5)/(52 c 13) + (13 c 3)(40 c 1)/(52 c 13)
Two players play the following game: Player A chooses one of the
three spinners pictured in Figure 2.6, and then player B chooses one
of the remaining two spinners. Both players then spin their spinner,
and the one that lands on the higher number is declared the winner.
Assuming that each spinner is equally likely to land in any of its 3
regions, would you rather be player A or player
B? Explain your answer!
Player B. If Player A chooses spinner (a) then B can choose spinner
(c). If A chooses (b)
then B chooses (a). If A chooses (c) then
B chooses (b). In each case B wins probability 5/9.