physics ch 6 Flashcards

1) A box of mass m is pulled with a constant acceleration a along a horizontal frictionless floor by
a wire that makes an angle of 15° above the horizontal. If T is the tension in this wire, then
A) T = ma.
B) T > ma.
C) T < ma.

Two objects, each of weight W, hang vertically by spring scales as shown in the figure. The pulleys and the strings attached to the objects have negligible weight, and there is no appreciable friction in the pulleys. The reading in each scale is

A) W.
B) more than W, but not quite twice as much.
C) less than W.
D) 2W.
E) more than 2W.

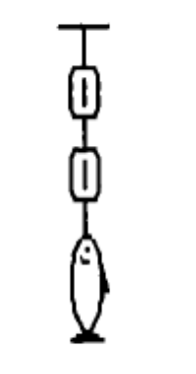
A fish weighing 16 N is weighed using two spring scales, each of negligible weight, as shown
in the figure. What will be the readings of the scales?

A) The bottom scale will read 16 N, and the top scale will read zero.
B) Each scale will read 16 N.
C) The top scale will read 16 N, and the bottom scale will read zero.
D) The scales will have different readings, but the sum of the two readings will be 16 N.
E) Each scale will read 8 N.

Two objects have masses m and 5m, respectively. They both are placed side by side on a
frictionless inclined plane and allowed to slide down from rest.
A) It takes the lighter object 5 times longer to reach the bottom of the incline than the
heavier object.
B) It takes the lighter object 10 times longer to reach the bottom of the incline than the
heavier object.
C) It takes the heavier object 5 times longer to reach the bottom of the incline than the
lighter object.
D) It takes the heavier object 10 times longer to reach the bottom of the incline than the
lighter object.
E) The two objects reach the bottom of the incline at the same time.

A box slides down a frictionless plane inclined at an angle θ above the horizontal. The
gravitational force on the box is directed
A) parallel to the plane in the same direction as the movement of the box.
B) parallel to the plane in the opposite direction as the movement of the box.
C) perpendicular to the plane.
D) vertically.
E) at an angle θ below the inclined plane.

A brick is resting on a rough incline as shown in the figure. The friction force acting on the
brick, along the incline, is

A) zero.
B) equal to the weight of the brick.
C) greater than the weight of the brick.
D) less than the weight of the brick.

7) When a parachutist jumps from an airplane, he eventually reaches a constant speed, called the
terminal speed. Once he has reached terminal speed
A) his acceleration is equal to g.
B) the force of air drag on him is equal to zero.
C) the force of air drag on him is equal to g.
D) his speed is equal to g.
E) the force of air drag on him is equal to his weight.

1) A block lies on a horizontal frictionless surface. A horizontal force of 100 N is applied to the
block giving rise to an acceleration of 3.0 m/s2.
(a) Determine the mass of the block.
(b) Calculate the distance the block will travel if the force is applied for 10 s.
(c) Calculate the speed of the block after the force has been applied for 10 s.

2) The following four forces act on a 4.00 kg object:
F1 = 300 N east
F2 = 700 N north
F3 = 500 N west
F4 = 600 N south
What is the acceleration of the object?
A) 224 N in a direction 63.4° north of west
B) 300 N in a direction 63.4° north of west
C) 300 N in a direction 26.6° north of west
D) 224 N in a direction 26.6° north of west
E) 2100 N in a direction 26.6° north of west

3) A 50.0-N box is sliding on a rough horizontal floor, and the only horizontal force acting on it is
friction. You observe that at one instant the box is sliding to the right at 1.75 m/s and that it
stops in 2.25 s with uniform acceleration. What magnitude force does friction exert on this box?
A) 3.97 N
B) 8.93 N
C) 38.9 N
D) 50.0 N
E) 490 N

A block is on a frictionless horizontal table, on earth. This block accelerates at 1.9 m/s2 when a
90 N horizontal force is applied to it. The block and table are then set up on the moon where
the acceleration due to gravity is 1.62 m/s2. What is the weight of the block on the moon?
A) 77 N
B) 67 N
C) 58 N
D) 48 N
E) 39 N

5) A block is on a frictionless horizontal table, on earth. This block accelerates at 3.6 m/s2 when a
90 N horizontal force is applied to it. The block and table are then set up on the moon where
the acceleration due to gravity is 1.62 m/s2. A horizontal force of 45 N is applied to the block
when it is on the moon. What acceleration does this force impart to the block?
A) 1.8 m/s2
B) 1.6 m/s2
C) 2.0 m/s2
D) 2.2 m/s2
E) 2.3 m/s2

A 10,000-kg rocket blasts off from earth with a uniform upward acceleration of 2.00 m/s2 and
feels no air resistance. The upward thrust force its engines must provide during this
acceleration is closest to
A) 20,000 N.
B) 980,000 N.
C) 118,000 N.
D) 78,000 N.

15) Bumpers on cars are not of much use in a collision. To see why, calculate the average force
a bumper would have to exert if it brought a 1200-kg car (a so-called compact model) to a rest
in 15 cm when the car had an initial speed of 2.0 m/s (about 4.5 mph). (Bumpers are built with
springs that compress to provide a stopping force without, hopefully, denting the metal.)
A) 1.8 × 104 N
B) 1.6 × 104 N
C) 5.4 × 104 N
D) 6.5 × 105 N
E) 3.2 × 104 N

8) A box of mass 50 kg is at rest on a horizontal frictionless surface. A constant horizontal force F
then acts on the box and accelerates it to the right. It is observed that it takes the box 6.9
seconds to travel 28 meters. What is the magnitude of the force?

A 1000-kg car is driving toward the north along a straight horizontal road at a speed of 20.0
m/s. The driver applies the brakes and the car comes to a rest uniformly in a distance of 200 m.
What are the magnitude and direction of the net force applied to the car to bring it to rest?
A) 1.00 N north
B) 10.0 × 103 N south
C) 1.00 × 103 N south
D) 1.00 N south
E) 100 N south

A construction worker pulls a box of tools on a smooth horizontal floor with a force of 100 N
in a direction of 37.0° above the horizontal. The mass of the box and the tools is 40.0 kg.
(a) Draw a free-body diagram for the box.
(b) Calculate the acceleration of the box.
(c) How hard does the floor push up on the box?

A 60.0-kg person rides in an elevator while standing on a scale. The scale reads 400 N. The
acceleration of the elevator is closest to
A) 3.13 m/s2 downward.
B) 6.67 m/s2 downward.
C) zero.
D) 9.80 m/s2 downward.
E) 6.67 m/s2 upward.

A 60.0-kg person rides in elevator while standing on a scale. The elevator is traveling
downward but slowing down at a rate of 2.00 m/s 2. The reading on the scale is closest to
A) 589 N.
B) 708 N.
C) 469 N.
D) 120 N.
E) 349 N.

A block is given a very brief push up a 20.0° frictionless incline to give it an initial speed of
12.0 m/s.
(a) How far along the surface of the plane does the block slide before coming to rest?
(b) How much time does it take to return to its starting position?

A 50.0-kg box rests on a horizontal surface. The coefficient of static friction between the box
and the surface is 0.300 and the coefficient of kinetic friction is 0.200. What is the friction force
on the box if
(a) a horizontal 140-N push is applied to it?
(b) a horizontal 175-N push is applied to it?

15) In a shuffleboard game, the puck slides a total of 12 m before coming to rest. If the coefficient
of kinetic friction between the puck and the horizontal board is 0.28, what was the initial speed
of the puck?
A) 8.1 m/s
B) 29.0 m/s
C) 6.5 m/s
D) 7.3 m/s

A driver in a 1000 kg car traveling at 20 m/s slams on the brakes and skids to a stop. If the
coefficient of friction between the tires and the horizontal road is 0.80, how long will the skid
marks be?
A) 26 m
B) 21 m

17) Jason takes off from rest across level water on his jet-powered skis. The combined mass of
Jason and his skis is 75 kg (the mass of the fuel is negligible). The skis have a thrust of 200 N
and a coefficient of kinetic friction on water of 0.10. Unfortunately, the skis run out of fuel after
only 48 s. What is Jasonʹs top speed?
A) 81 m/s
B) 130 m/s
C) 13 m/s
D) 48 m/s

18) Jason takes off from rest across level water on his jet-powered skis. The combined mass of
Jason and his skis is 75 kg (the mass of the fuel is negligible). The skis have a thrust of 200 N
and a coefficient of kinetic friction on water of 0.10. Unfortunately, the skis run out of fuel after
only 67 s. How far has Jason traveled when he finally coasts to a stop?
A) 10,000 m
B) 7600 m
C) 5400 m
D) 3800 m

19) Kieran takes off from rest down a 50 m high, 10 ° slope on his jet-powered skis. The skis have a
thrust of 280 N parallel to the surface of the slope. The combined mass of skis and Kieran is 50
kg (the fuel mass is negligible). Kieranʹs speed at the bottom is 40 m/s. What is the coefficient
of kinetic friction of his skis on snow?
A) 0.47
B) 0.58
C) 0.23
D) 0.29

A factory robot drops a 10 kg computer onto a conveyor belt running at 3.1 m/s. The materials
are such that μs = 0.50 and μk = 0.30 between the belt and the computer. How far is the
computer dragged before it is riding smoothly on the belt?
A) 1.6 m
B) 0.98 m
C) 2.3 m
D) 3.0 m

You push downward on a box at an angle 25° below the horizontal with a force of 750 N. If the
box is on a flat horizontal surface for which the coefficient of static friction with the box is 0.76,
what is the mass of the heaviest box you will be able to move?
A) 59 kg
B) 68 kg
C) 54 kg
D) 82 kg

A person is dragging a packing crate of mass 100 kg across a rough horizontal floor where the
coefficient of kinetic friction is 0.400. He exerts a force F sufficient to accelerate the crate
forward. At what angle above horizontal should his pulling force be directed in order to
achieve the maximum acceleration?
A) 21.8°
B) 27.7°
C) 30°
D) 34.5°
E) 45°

23) A packing crate rests on a horizontal surface. It is acted on by three horizontal forces: 600 N to
the left, 200 N to the right, and friction. The weight of the crate is 400 N. If the 600-N force is
removed, the resultant force acting on the crate is
A) zero.
B) 200 N to the right.
C) 200 N to the left.
D) 400 N to the left.
E) impossible to determine from the information given.

A 6.0 kg box slides down an inclined plane that makes an angle of 39 ° with the horizontal. If
the coefficient of kinetic friction is 0.19, at what rate does the box accelerate down the slope?
A) 4.7 m/s2
B) 5.2 m/s2
C) 5.5 m/s2
D) 6.2 m/s2

25) A 200 g hockey puck is launched up a metal ramp that is inclined at a 30° angle. The
coefficients of static and kinetic friction between the hockey puck and the metal ramp are μs =
0.40 and μk = 0.30, respectively. The puckʹs initial speed is 63 m/s. What vertical height does
the puck reach above its starting point?
A) 130 m
B) 270 m
C) 200 m
D) 66 m

A 200 g hockey puck is launched up a metal ramp that is inclined at a 30° angle. The
coefficients of static and kinetic friction between the hockey puck and the metal ramp are μs =
0.40 and μk = 0.30, respectively. The puckʹs initial speed is 4.9 m/s. What speed does it have
when it slides back down to its starting point?
A) 2.8 m/s
B) 3.5 m/s
C) 4.2 m/s
D) 4.9 m/s

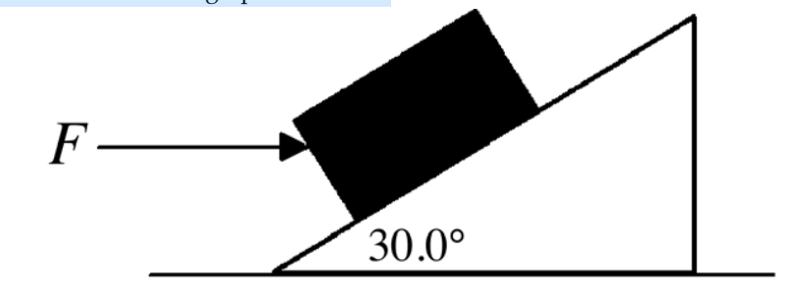
A 4.00-kg block rests on a 30.0° incline as shown in the figure. If the coefficient of static
friction between the block and the incline is 0.700, what magnitude horizontal force F must act
on the block to start it moving up the incline?

A box is sliding down an incline tilted at a 12.0° angle above horizontal. The box is initially
sliding down the incline at a speed of 1.50 m/s. The coefficient of kinetic friction between the
box and the incline is 0.340. How far does the box slide down the incline before coming to
rest?
A) 0.920 m
B) 2.33 m
C) 1.78 m
D) 0.720 m
E) The box does not stop. It accelerates down the plane.

29) A 50.0-kg block is being pulled up a 16.0° slope by a force of 250 N which is parallel to the
slope. The coefficient of kinetic friction between the block and the slope is 0.200. What is the
magnitude of the acceleration of the block?
A) 0.528 m/s2
B) 0.158 m/s2
C) 0.412 m/s2
D) 0.983 m/s2
E) 0.260 m/s2

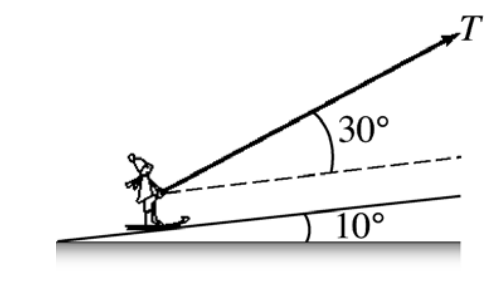
In the figure, a T-bar ski tow pulls a skier up a hill inclined at 10° above horizontal. The skier
starts from rest and is pulled by a cable that exerts a tension T at an angle of 30° above the
surface of the hill. The mass of the skier is 60 kg and the effective coefficient of kinetic friction
between the skis and the snow is 0.100. What is the maximum tension in the cable if the
starting acceleration is not to exceed 0.400 g?

A) 246 N
B) 366 N
C) 431 N
D) 187 N
E) 535 N

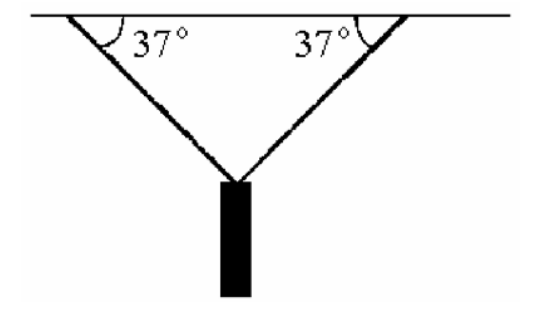
A traffic light weighing 100 N is supported by two ropes as shown in the figure. The tensions
in the ropes are closest to

A) 50 N.
B) 56 N.
C) 63 N.
D) 66 N.
E) 83 N.

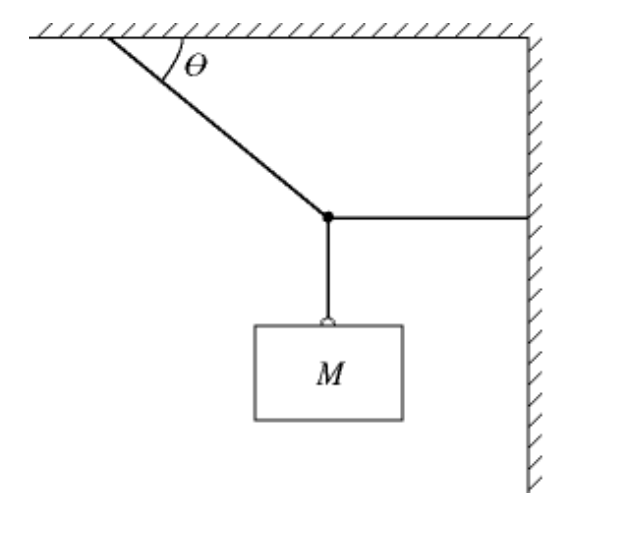
In the figure, a block of mass M hangs at rest. The rope that is fastened to the wall is horizontal
and has a tension off 52 N. The rope that is fastened to the ceiling has a tension of 91 N,and
makes an angle θ with the ceiling. What is the angle θ?

A) 55°
B) 35°
C) 30°
D) 63°
E) 45°

34) The magnitude of the drag force of air resistance on a certain 20.0-kg object is proportional to
its speed. If the object has a terminal speed 80.0 m/s, what is the magnitude of the drag force
on the object when it is falling with a speed 30.0 m/s?
A) 196 N
B) 7.50 N
C) 15.0 N
D) 73.5 N
E) 42.7 N

A 30.0-kg object experiences a drag force due to air resistance with a magnitude proportional
to the square of its speed. The object falls with an acceleration of 4.00 m/s 2 downward when it
is falling downward at 70.0 m/s. What is its terminal speed?
A) 110 m/s
B) 157 m/s
C) 91.0 m/s
D) 172 m/s
E) 108 m/s

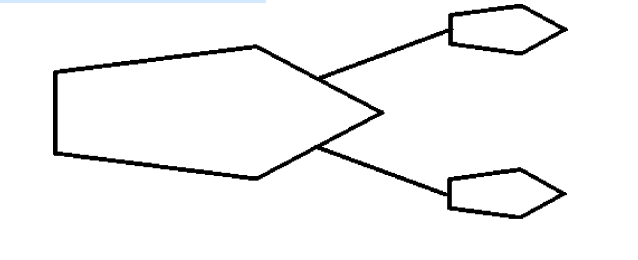
A ship is being pulled through a harbor at constant velocity by two tugboats as shown in the
figure. The lines attached to the two tugboats have the same tension of 200,000 N. Each line
makes an angle of 28.0° with the direction the ship is being towed. What is the magnitude of
the drag force due to the water on the ship?

A) 177 × 105 N
B) 1.88 × 105 N
C) 93.9 × 104 N
D) zero
E) 3.53 × 105 N

37) A 1.20-kg ball is hanging from the end of a rope. The rope hangs at an angle 25.0° from the
vertical when a 15.0 m/s horizontal wind is blowing. If the windʹs force on the rope is
negligible, what drag force does the wind exert on the ball?
A) 32.3 N
B) 24.1 N
C) 3.68 N
D) 5.48 N
E) 11.8 N

38) An 80.0-kg object is falling and experiences a drag force due to air resistance. The magnitude
of this drag force depends on its speed, v, and obeys the equation
Fdrag = (12.0 N · s/m)v + (4.00 N · s2/m2)v2. What is the terminal speed of this object?
A) 6.45 m/s
B) 72.2 m/s
C) 34.2 m/s
D) 12.6 m/s
E) 47.3 m/s

39) An object weighing 4.00 N falls from rest subject to a frictional drag force given by Fdrag =
bv2, where v is the speed of the object and b = 3.00 N · s2/m2. What terminal speed will this
object approach?
A) 1.78 m/s
B) 3.42 m/s
C) 1.15 m/s
D) 2.25 m/s
E) 0.75 m/s