Classify each of the following statements as a hypothesis, theory, or law.

A hypothesis is an educated guess, or an untested explanation, that is based upon observations or know facts. For example, if an entomologist guesses that gray moths survive better on gray tree trunks, he or she has constructed a hypothesis. This hypothesis can be tested in one or more experiments or tests.
If a hypothesis has been repeatedly tested and has not been disproved, it may become accepted as a theory. Examples include cell theory and atomic theory.
A law describes what happens, but does not explain how it happens. One example is the law of gravity.
Which of the following are chemical changes? Check all that apply.

The only chemical change in the list is <"gasoline is burned>".
When water is heated up, energy is added to the system, but there are no chemical changes.
The other three changes are all phase changes.
Give the SI base unit of each of these quantities. Enter the abbreviation rather than the name of the unit.

The SI base unit of mass is the kilogram, kg.
The SI base unit of length is the meter, m.
The SI base unit of time is the second, s.
Identify the power of ten that defines each of these prefixes.

The powers of ten that define each of these prefixes are:
nano- 10^-9
kilo- 10^3
centi- 10^-2
micro- 10^-6
milli- 10^-3
mega- 10^6
Write the following numbers in scientific notation.

673.5 = 6.735 × 10^2
0.034 = 3.4 × 10^-2
Rank these values according to magnitude.

First, rank the values by exponent:
2.3 × 10^5
6.5 × 10^4
3.0 × 10^–2
9.0 × 10^–6 and 8.3 × 10^–6
To rank the two values with the same exponent, look at the coefficient.
9.0 > 8.3 and so 9.0 × 10^–6 > 8.3 × 10^–6.
Convert the following length to its equivalent in nanometers.
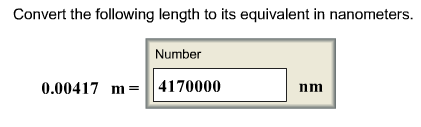
A nanometer is a billionth of a meter:
1 nm = 10^-9 m
which gives us two possible conversion factors:
(1 nm / 10^-9 m) OR (10^-9 m / 1 nm)
We are given a value in meters, and we want m to cancel out, so we choose the first conversion factor.
.00417 m x (1 m / 10^-9 nm)= 4170000 nm

Convert the following volume to its equivalent in milliliters:


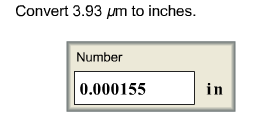
Convert 3.93 μm to inches.
Each of the measurements below describes length. Rank them from longest length to shortest length.

It is easier to rank these by first converting them to a single unit. An example conversion (to meters) is worked below:
The necessary conversion factor for this example is 1 mi = 1609.344 m.
1 mi x (1609.344 m / 1 mi ) = 1609 m
Therefore, the ranking in units of meters is
1609 m > 100 m > 10 m > 1.3 m
The measurements are, from longest to shortest:
1 mi > 1 × 1011 nm > 10 m > 50 in

Liquid helium boils at –268.93 °C. What is the boiling point of helium on the Kelvin temperature scale?


Many bacteria, such as E. coli, thrive at body temperature, 37.0 °C; therefore, bacteria are grown in laboratories at that temperature. What is the corresponding Fahrenheit temperature?

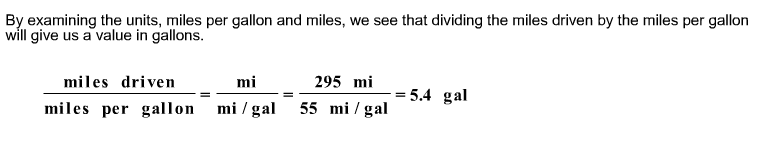
A certain hybrid car has a mileage rating of 55 miles per gallon. If the car makes a trip of 295 miles, how many gallons of gasoline will be used?


If a bullet travels at 639.0 m/s, what is its speed in miles per hour?

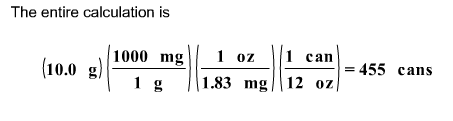
If the caffeine concentration in a particular brand of soda is 1.83 mg/oz, drinking how many cans of soda would be lethal? Assume 10.0 grams of caffeine is a lethal dose, and there are 12 oz in a can.

First, we calculate the number of mg of caffeine in a can of soda.
(1.83 mg / 1 oz.) x (12 oz. / 1 can) = 22 mg / can
Next, we determine the number of grams of caffeine in a can of soda.
(22 mg / 1 can) x (1g / 1000 mg) = .0220 g / can
Finally, we determine the number of cans needed to obtain 10.0 g of caffeine.
100 g x (1 can / .0220 g) = 455 cans