rx-axis
(x, - y)
x is lazy & doesn't change
ry-axis
(-x, y)
y is lazy & doesn't change
ry=x
(y,x)
switch order
ry = - x
(-y, -x)
switch & negate
RO,90
(- y, x)
RO, 180
(-x, -y)
RO, 270
(y, -x)
Ta,b
(x+a, y+b)
rorigin
(-x,-y)
Golden Rule for Rigid Motion Explanation as to why 2 triangles are congurent
A series of rigid motions (you list the specific ones you did in the problem) MAPS shape 1 onto shape 2. Rigid motions preserve segment length and angle measure, therefore the image is congruent to the pre-image.
Line reflection
is the Perpendicular Bisector of the line segment connecting each pre-image point to its image.
Orientation
The arrangement (or how you name the shape) of the points before and after a transformation.
If it is preserved, the order and direction will be the same in the pre-image and the image.
Orientation NOT is preserved for what type of transformation?
a line reflection
what does the line x = # look like?
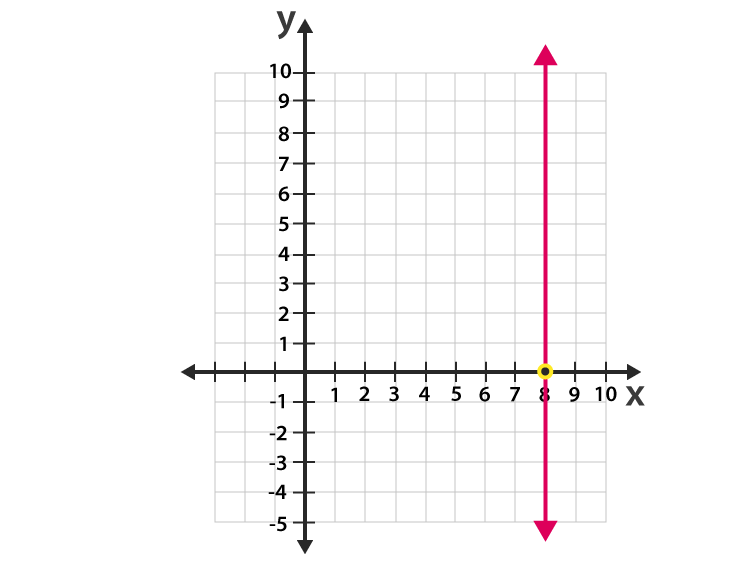
a Vertical line
what does the line y = # look like?
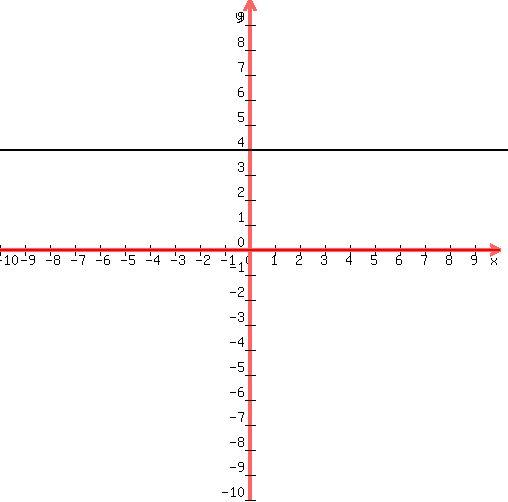
a Horizontal line
Rotation notation must have three things: CDD
C: Center of Roation
D: Direction of Rotation ( + = Counter clockwise (CCW) & - = clockwise (CW))
D: Degree of Rotation
EX: RO,-90

Theta = angle measurement symbol
Regular Polygons
A shape with ALL SIDES CONGRUENT & ALL ANGLES CONGRUENT
Regular Pentagon
5 sides
Regular HeXagon
siX sides
Regular Heptagon
7 sides
Regular Octogon
8 sides
Regular Nonagon
9 sides
Regular Decagon
10 sides
Regular Dodecagon
12 sides
Point Symmetry
If you turn a shape upside down (or RO, 180) and it looks the same, then it has point symmetry
Roational Symmetry
The number of degrees less than 360 it takes to map a shape onto itself.
If your shape is a regular polygon then the formula to find the rotational symmetry is: 360/ n (where n is the number of sides)
Line Symmetery
the "Fold Line" that divides a shape into 2 identical halves
Composition Notation
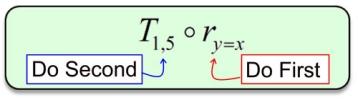
**Work Backwards**