Graph
consists of points (called vertices or nodes) which are connected by lines (edges or arcs)
Weighted graph / network
A graph where the edges have associated values (weights)
Vertex set

A, B, C, D, E, F, the vertices within a graph
Edge set

AD, AE, BA, BC, CE, CF, DE, EF, the edges within the graph (G)
Subgraph of G
A graph, each of whose vertices belong to the original graph (G) and each of whose edges belong to G. It is simply a part of the original graph.
Degree, Order, or Valency of a vertex

The no. of edges incident to the vertex
A: 3, B: 2 etc.
Even vertex
vertex with an even degree
Odd vertex
vertex with an odd degree
Walk
A route through a graph along edges and from one vertex to another (can be multiple vertices and edges)
Path
A walk where no vertex is visited more than once
Trail
A walk where no edge is visited more than once
Cycle
A walk where the end vertex is the same as the start vertex and no vertex is visited more than once
Hamiltonian cycle
A cycle which includes every vertex.
Connected graph
Where every vertex is connected, in some way, to the graph. (Vertices are connected when there is an arc connecting them)
Loop
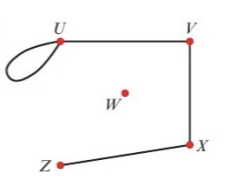
Edge that starts and finishes at the same vertex
Simple graph
A graph with no loops and up to one arc connecting the same two vertex
Directed graph
Graphs where direction is associated to each arc, often shortened to digraph
The Handshake Lemma
Th sum of the degrees of the vertices is equal to 2x the number of edges, as a consequence the number of vertices must be even. This is known as Euler's Handshake Lemma.