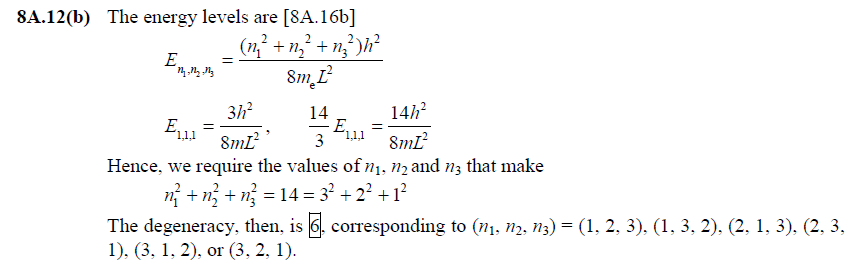[8A.2] Describe the features of the solution of the particle in a one-dimensional box that appear in the solutions of the particle in two- and three-dimensional boxes. What concept applies to the latter but not to a one-dimensional box.

[8A.1(b)] Determine the linear momentum and kinetic energy of a free proton described by the wavefunction e^−ikx with k=5nm−1.

[8A.3(b)] Calculate the energy separations in joules, kilojoules per mole, electronvolts, and reciprocal centimetres between the levels (i) n = 3 and n = 1, (ii) n = 7 and n = 6 of an electron in a box of length 1.50 nm.

[8.4(b)] Calculate the probability that a particle will be found between 0.65L and 0.67L in a box of length L when it has (i) n = 1, (ii) n = 2. Take the wavefunction to be a constant in this range.


[8A.7(b)]
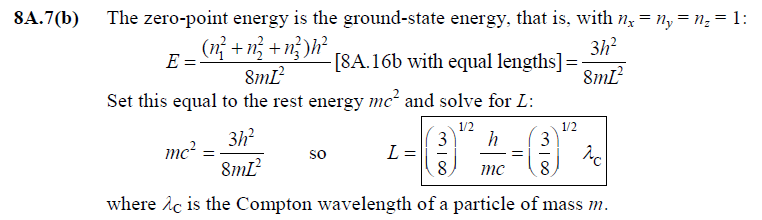

[8A.11(b)]

surprised to find degeneracy in a box with unequal lengths. Symmetry
is a matter of degree.
This box is less symmetric than a square
box, but it is more symmetric than boxes whose
sides have a
non-integer or irrational ratio. Every state of a square box except
those with
n1=n2 is degenerate (with the
state that has n1 and n2 reversed). Only a few
states in this box
are degenerate. In this system, a state
(n1, n2) is degenerate with a state
(n2/2, 2n1) as long as
the latter state (a) exists
(i.e., n2/2 must be an integer) and (b) is distinct from
(n1, n2). A box
with incommensurable sides,
say, L and 21/2L, would have no degenerate levels.
[8A.12(b)]