Print Options

Card layout: ?

← Back to notecard set|Easy Notecards home page

Instructions for Side by Side Printing
  1. Print the notecards
  2. Fold each page in half along the solid vertical line
  3. Cut out the notecards by cutting along each horizontal dotted line
  4. Optional: Glue, tape or staple the ends of each notecard together
  1. Verify Front of pages is selected for Viewing and print the front of the notecards
  2. Select Back of pages for Viewing and print the back of the notecards
    NOTE: Since the back of the pages are printed in reverse order (last page is printed first), keep the pages in the same order as they were after Step 1. Also, be sure to feed the pages in the same direction as you did in Step 1.
  3. Cut out the notecards by cutting along each horizontal and vertical dotted line
To print: Ctrl+PPrint as a list

7 notecards = 2 pages (4 cards per page)

Viewing:

CHAPTER 8A Problem Solving

front 1

[8A.2] Describe the features of the solution of the particle in a one-dimensional box that appear in the solutions of the particle in two- and three-dimensional boxes. What concept applies to the latter but not to a one-dimensional box.

back 1

front 2

[8A.1(b)] Determine the linear momentum and kinetic energy of a free proton described by the wavefunction e^−ikx with k=5nm−1.

back 2

front 3

[8A.3(b)] Calculate the energy separations in joules, kilojoules per mole, electronvolts, and reciprocal centimetres between the levels (i) n = 3 and n = 1, (ii) n = 7 and n = 6 of an electron in a box of length 1.50 nm.

back 3

front 4

[8.4(b)] Calculate the probability that a particle will be found between 0.65L and 0.67L in a box of length L when it has (i) n = 1, (ii) n = 2. Take the wavefunction to be a constant in this range.

back 4

front 5

[8A.7(b)]

back 5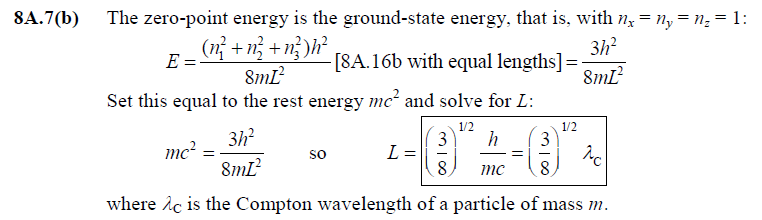

front 6

[8A.11(b)]

back 6

surprised to find degeneracy in a box with unequal lengths. Symmetry is a matter of degree.
This box is less symmetric than a square box, but it is more symmetric than boxes whose
sides have a non-integer or irrational ratio. Every state of a square box except those with
n1=n2 is degenerate (with the state that has n1 and n2 reversed). Only a few states in this box
are degenerate. In this system, a state (n1, n2) is degenerate with a state (n2/2, 2n1) as long as
the latter state (a) exists (i.e., n2/2 must be an integer) and (b) is distinct from (n1, n2). A box
with incommensurable sides, say, L and 21/2L, would have no degenerate levels.

front 7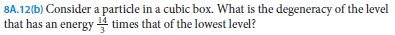

[8A.12(b)]

back 7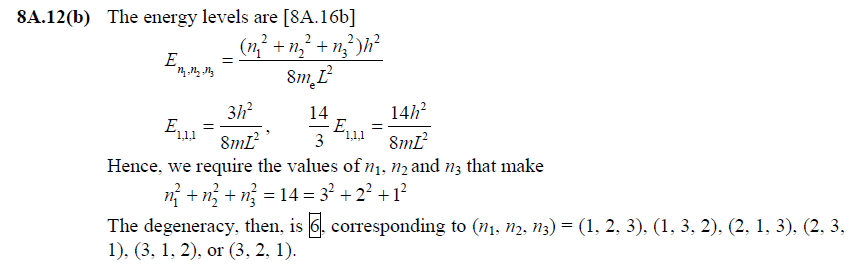