graph

Points (called vertices or nodes) which are connected by lines (edges or arcs)

weighted graph/network

if a graph has a number associated with each edge (usually called its weight) then it is a weighted graph or a network

vertex set

list of all the nodes on a graph

e.g. A,B,C,D,E

edge set

list of all the edges in a graph (AB, AC, etc...)

subgraph

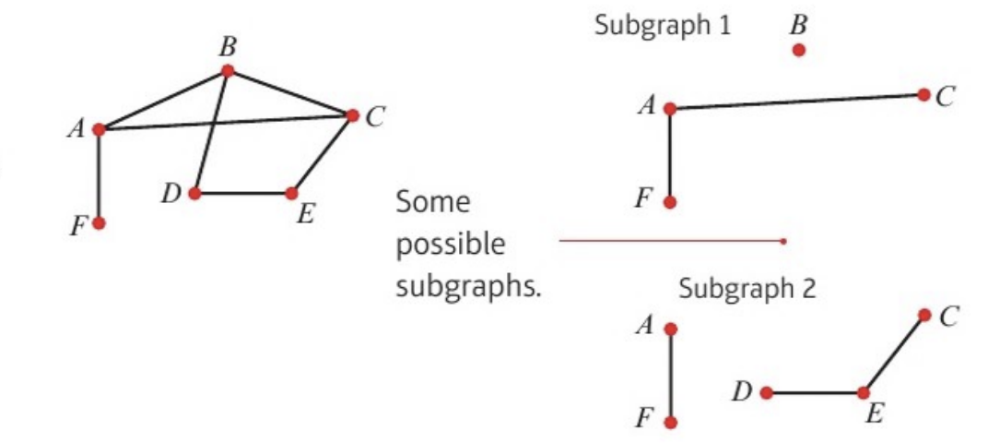
A subgraph of (e.g.) graph G is a graph where each of whose vertices belongs to G - it is simply a part of the original graph

(graph on left is graph G, graphs on right are subgraphs of graph G)

degree/valency/order of a vertex

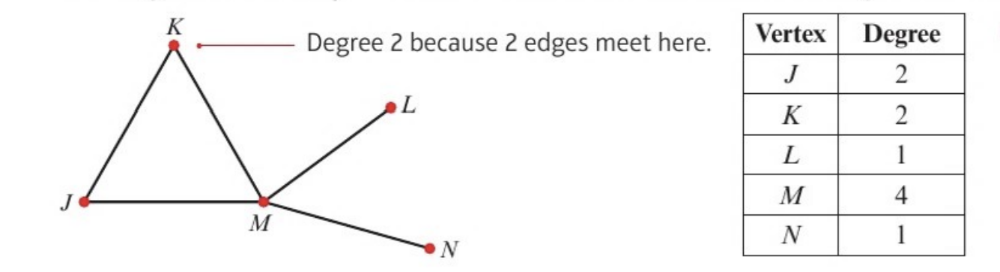
number of edges incident to that vertex

if a vertex has even degree we say it is even and if it has odd degree we say it is an odd vertex

walk

a route through a graph along edges from one vertex to the next

path

a walk in which no vertex is visited more than once

trail

a walk in which no edge is visited more than once

cycle

a walk in which the end vertex is the same as the start vertex and no other vertex is visited more than once

Hamiltonian cycle

a cycle* which includes every vertex

_{*cycle=a walk in which the end vertex is the same as the start vertex and no other vertex is visited more than once}

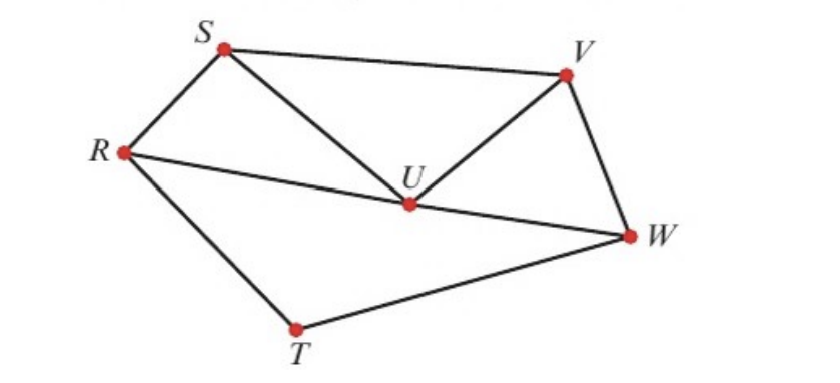
in terms of the diagram, give examples of:

1. a walk

2. a path

3. a trail

4. a cycle

5. an hamiltonian cycle

walk: e.g. RSUWVU, SUV, etc

path: RSUVW, RUVW, etc

trail: RUSVUW

cycle: RSUR

hamiltonian cycle: RSUVWTR

connected vs unconnected graphs

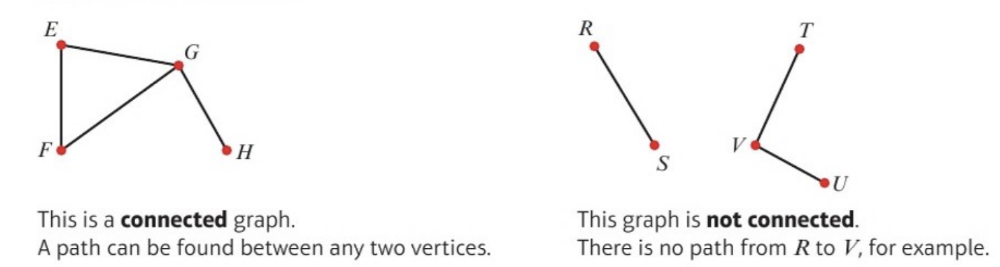
Two vertices are connected if there is a path between them. a graph is connected if all its vertices are connected

loop

an edge that starts and finishes at the same vertex

simple graph

graph in which there are no loops and there is at most one edge connecting any pair of vertices

digraph

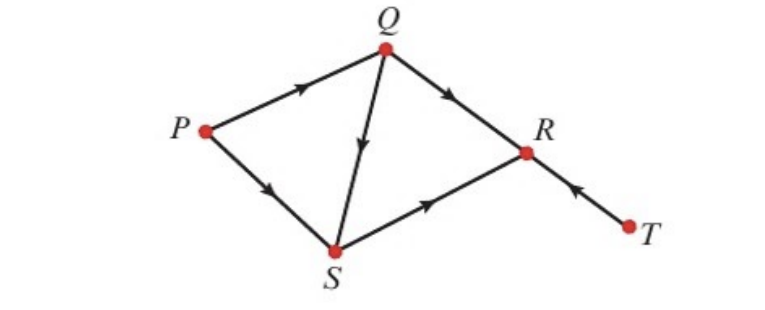
if the edges of a graph have a direction associated with them they are known as directed edges and the graph is known as a directed graph (digraph)

Euler's handshaking lemma

In any undirected graph, the sum of the degrees of the vertices is equal to 2x the number of edges.

Therefore, the number of odd vertices must always be even (including possibly zero). This result is known as Euler's handshaking lemma.