The goal of an integrated rate law is to have an expression for the concentration of either the reactants or the products as a function of _________ . In general, they are most useful when the rate of the reactions depends on __________ chemical species.
Time : 1
Consider the reaction below:
2N2O (g) → 2N2 (g) + O2 (g)
It has a rate law of:
rate = k[N2O]
where k = 6.8 x 10–3 s–1
The integrated rate law for this reaction tells us that...
The concentration of N2O decreases exponentially with time.
Yes, the integrated rate law for this reaction would be: [N2O](t) = [N2O]initiale–kt which means that N2O decreases exponentially with time.
Consider the reaction:
2N2O (g) → 2N2 (g) + O2 (g)
It has a rate law of:
rate = k[N2O]
Given the two forms of the integrated law for first order kinetics and your understanding of how N2O should change with time calculate the time in seconds required for the concentration of N2O (g) to decrease from 0.75 M to 0.33 M. The rate constant for this reaction is
k = 6.8 x 10–3 s–1
121 seconds
Yes. You could use either form of the integrated rate law to solve for time, t.
For example:
ln[A]t = ln[A]0 – kt
ln(0.33M) = ln(0.75M) – (0.0068 s–1)(t)
t ≈ 121 seconds
A non-steroidal anti-inflammatory drug is metabolized with a first-order rate constant of 3.25 day-1. What is the half-life for the metabolism reaction?
0.213
Yes. Recall that the equation for first order half-life is t = ln(2)/k.
For our example:
t = ln(2)/(3.25 day–1) = 0.693/(3.25 day–1) = 0.213 day
The half life of a species that undergoes zero order kinetics is ____ and the rate constant has units of ____.
Half life = (A)o/2k ; Ms-1
Yes. The half-life of a species undergoing zero order decay has is [A]0/2k and the units of the rate constant k are M/s.
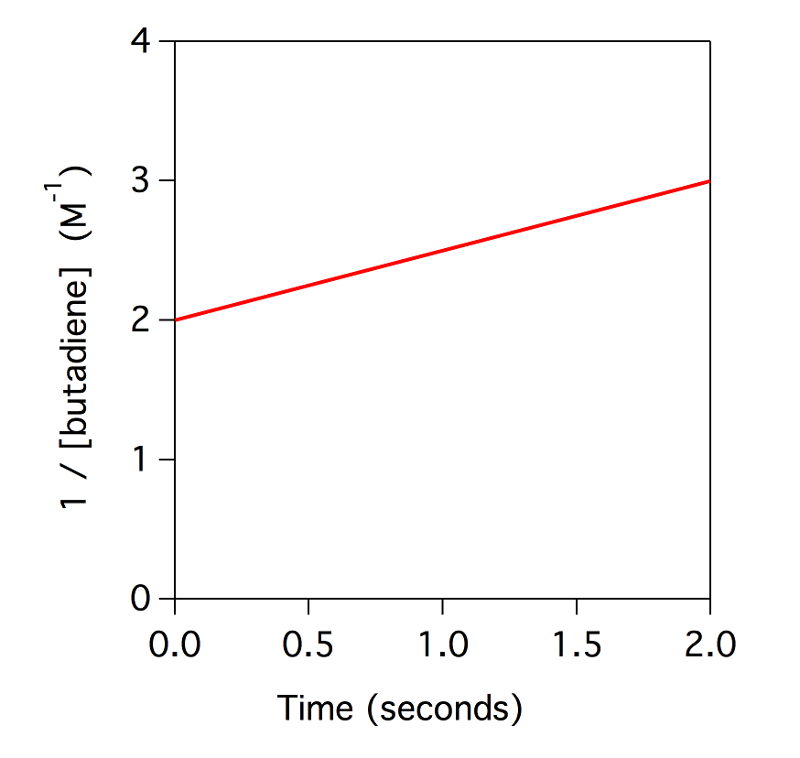
The plot below shows the kinetics for the dimerization of butadiene. What is the value of the rate constant?
0.5 M–1s–1
Yes. This is a second order reaction. Therefore, the slope of the plot 1/[butadiene] versus time gives the value of the rate constant.
Consider the following reaction and its respective rate law and constant:
CH2O (g) + O2 (g) → CO2 (g) + H2O (g)
rate = k[O2]2
k = 5.4 x 104 M–1s–1
If there is initially 1.334 M O2, how long will it take for the O2 concentration to reach 0.443 M?
28 µs
Yes. This is second order kinetics so we need to use the integrated rate law for second order kinetics. Our [A]0 value is 1.334 M and our [A] value is 0.443 M, we also know the rate constant. So let's input the values and solve for t:
[A]t–1 = [A]0–1 + kt
(0.443M)–1 = (1.334M)–1 + (5.4 x 104 M–1s–1)t
2.257 M–1 = 0.750 M–1 + (5.4 x 104 M–1s–1)t
1.51 M–1 = (5.4 x 104 M–1s–1)t
t = 0.000028 seconds = 28 microseconds = 28 µs
The following reaction
A + B → C
is found to follow the rate law
rate = k[A][B]
when will a plot of ln[A] vs time yield a straight line?
when the [B]>>[A]
Yes. If the concentration of B is very high it will essentially be constant. Then the reaction will appear first order in A. This is the pseudo-first order condition.
Which of the following is NOT true about chemical mechanisms?
A proposed mechanism always matches the measured rate law.
Yes. Mechanisms are always subject to further study and evidence. Sometimes the proposed mechanism doesn't match the measured rate law.
There exists some reaction written like this:
2A (g) → 4B (g) + C (g)
The mechanism is unknown but your friend writes an overall rate law like this:
rate = k[A]2
Is this overall rate law accurate?
It might be, but you cannot tell from the information given.
Yes, without the mechanism we don't know the overall rate law. We can write the rate laws for individual elementary steps using the stoichiometric coefficients of the elementary steps. Without a known mechanism, however, we cannot do the same with an overall reaction.
A mechanism for the decomposition of ozone (2O3 → 3O2 ) is
O3 → O2 + O
O + O3 → O2 + O2
What is the molecularity for the first and second elementary reactions?
(1 = unimolecular , 2= bimolecular)
1 and 2
Yes. The first step depends on only one reactant. The second step depends on two reactants.
For a multistep reaction, the rate of the reaction is primarily determined by the
slowest step of the sequence.
Yes. The "rate limiting step" determines how the overall reaction will proceed.
What is the relationship between the equilibrium constant of a the fast step of a mechanism and the rate constants for the forward and back directions of the same fast step?
The equilibrium constant for this fast equilibrium step is the ratio of the forward rate constant to the backward rate constant.
Yes. This is a very important idea in chemistry!
Determine the overall balanced equation for a reaction having the following proposed mechanism
Step 1: B2 + B2 → E3 + D (slow)
Step 2: E3 + A → B2 + C2 (fast)
and write an acceptable rate law.
A + B2 → C2 + D
rate = k[B2]2
Yes. The slow step is the rate limiting step, so we begin writing our rate law with this step: rate = k[B2]2. Then we check that this rate law does not include any intermediates. It does not and so we can keep this as the overall rate law. To determine the overall reaction we add together the two elementary steps, simplify and eliminate any intermediates.
The reaction
2NO2 → 2NO (g) + O2 (g)
is postulated to occur via the mechanism
NO2 (g) + NO2 (g) → NO (g) + NO3 (g) (slow)
NO3 (g) → NO (g) + O2 (g) (fast)
What is an intermediate in this reaction?
NO3 (g)
Yes. NO3 is neither a reactant nor a product in the overall reaction. However, it does show up as a product and reactant int the elementary steps. Therefore it is an intermediate.
Here is a proposed mechanism (assume that all species are in the gas phase):
Step 1: 2NO ⇌ N2O2 (fast)
Step 2: N2O2 + O2 → 2NO2 (slow)
What is the rate law for the overall reaction?
rate = k[NO]2[O2]
Yes. We begin by writing the rate law from the slow step: rate = k[N2O2][O2] but we recognize that N2O2 is an intermediate because the overall reaction is 2NO + O2 → 2NO2
However, if we step up the equilibrium expression for step 1 we can replace it in our rate law: K = [N2O2]/[NO]2 therefore [N2O2]=K[NO]2 We can now replace [N2O2] with K[NO]2 and our rate law becomes rate = k[NO]2[O2] where the rate constant "k" now includes the original value of the rate law times the value of the equilibrium constant (K) for step 1.
In order to speed up the rate of a reaction, one can either ________ the temperature (Arrhenius Theory) or ______ the energy barrier of the reaction (catalysis).
Raise; Lower
Transition state theory attempts to explain reaction rates in term of
energetic differences between ground states and transition states.
Yes, transition state theory involves identifying the highest energy point along the lowest energy path.
All else being equal, a reaction with a higher activation energy compared to one with a lower activation energy will
proceed slower.
Yes. The rate is limited by the magnitude of energy barrier.
What is the value of the rate constant for the reaction
N2O → N2 + O
if the reaction occurs at room temperature with a pre-exponential factor of 8.2 x 1012 s–1 and an activation energy of 250 kJ/mol?
1.29 x 10–31
Yes. You can use one of two formulas to solve for the rate constant k. Let's use the exponential formula. First, we need to know room temperature in Kelvin: 298 K. Secondly, we need to recognize that our energy was given in kJ. We could either look up an R value in joules or use the commonly known R value 8.314 J/molK. If we use 8.314 J/molK we must convert 250 kJ into joules by multiplying by 1000 to get 250,000 J. Now we can calculate k:
k= (Ae^(-Ea/RT)) = (8.2x10^12)(-250000/e^8.314*298K)`
k≈1.29 x 10–31
For the reaction
HO (g) + H2 (g) → H2O (g) + H (g)
a plot of lnkvs1Tlnkvs1T gives a straight line with a slope equal to –5.1 x 103 K. What is the activation energy for the reaction?
42 kJ/mol
Yes. The linear relationship between ln(k) and 1/T is written: ln(k) = ln(A) – (Ea/R)(1/T) Analyzing the linear relationship, we find that the slope of the line is equal to –Ea/R. So we can take the value of the slope given and set it equal to –Ea/R:
–5.1x103 K= – Ea/(8.314 J/molK)
Ea = 42401.4 J/mol ≈ 42 kJ/mol
Now, consider this mechanism:
NO2 (g) + F2 (g) → NO2F (g) + F (g) (slow)
F (g) + NO2 (g) → NO2F (g) (fast)
What does the reaction profile show?
two maxima, the first being the highest
Yes. There are two steps in the mechanism which means there are two activation energy barriers along the reaction coordinate. The first step is the slow step, so it has the greatest barrier.
Which of the following is true of catalysts in general:
catalysts speed up very specific reactions
Yes, catalysts are selective.
A catalyst...
changes the mechanism of the reaction, lowering the activation energy.
Yes. This is the most important idea to remember about catalysts
Biological catalysts generally have similar overall mechanisms. Fill in the chemical reaction with the terms that describe the biological catalyst in action:
Substrate + Enzyme >>> Complex >>> Product
We __________ have oxidation in conjunction with reduction. Oxidation is _________ , and reduction _____________
Always; Loss of electrons; Gain of Electrons
In the redox conversion of Ni2+ to NiO4–, the oxidation number of Ni goes from _____ to _____. Recall that the oxidation number of oxygen is typically –2
+2; +7
Yes. The ion Ni2+ has a 2+ charge and that is its oxidation number as well. In the compound NiO4– each oxygen has an oxidation number of –2. There are four oxygen atoms which means they provide a –8 charge. Also, the overall charge of the compound is –1 which indicates that Ni must have a +7 oxidation number.
In the reaction
2Na (s) + Cl2 (g) → 2NaCl (s)
___?___ is(are) oxidized and ___?___ is(are) reduced.
Na; Cl
Na changes from an oxidation number of 0 to +1. What kind of process is this? Cl changes from an oxidation number of 0 to –1. What kind of process is this?
Select the true statement for the following reaction:
N2 (g) + 3H2 (g) → 2NH3 (g)
Each N atom is reduced from 0 to -3. Each H atom is oxidized from 0 to +1.
Both N and H start out in the their elemental forms with oxidation numbers of 0. Then in the products, H now has an oxidation number of +1. When a substance increases its oxidation number (becomes more positive), what type of process is this? There are three hydrogen atoms in the NH3 compound which means N must now be –3. When a substance decreases its oxidation number (becomes more negative), what type of process is this?
These two reactions are combined in a redox reaction:
(I) Cu → Cu2+
(II) Cr2O72– → Cr3+
Don't worry about balancing and combining them now. Just choose the correct statement below. Recall that the oxidation state of oxygen is usually -2.
The Cr is reduced from +6 to +3; the Cu is oxidized from 0 to +2.
Yes. In the chromium half-reaction, there are 7 O atoms each with an oxidation number of –2 in the reactant compound and the overall charge is –2. So the two chromium atoms must make up +12 charge to achieve the overall charge of the ion. This means that each Cr atom must have an oxidation number of +6. The copper starts out in its elemental form (oxidation number of zero) and moves to a 2+ ion form.
Iron reacts with oxygen especially rapidly in the presence of water to produce the familiar reddish brown rust according to the equation:
4Fe (s) + 3O2 (g) + ?H2O (l) → 2Fe2O3 (s)
where ?H2O represents a non-specific number of water molecules.
Identify the reducing agent in this reaction.
Fe
Iron is the substance being oxidized (from 0 to +3), therefore it is the reducing agent. The electrons produced in the oxidation of iron reduce the oxygen.
Sodium bisulfite converts bromine (Br2) to bromide (Br –). Sodium bisulfite is...
a reducing agent.
Yes. Br is reduced. The substance that converted it from Br2 to Br– caused the reduction, therefore it is the reducing agent.
Match the terms with its unit name and correct unit symbols. Not all the matching choices will be used.
Current: (Ampere, Columb C, Seconds)
Charge: (Ampere, Columb C, Seconds)
Time: (Ampere, Columb C, Seconds)
Ampere, Columb, Seconds
1 Faraday is
the charge in Coulombs carried by one mole of electrons.
Yes, 1 Faraday is the charge in Coulombs per one mole of electrons.
The reaction
2Ag+ (aq) + Fe (s) → Fe2+ (aq) + 2Ag (s)
takes place in a battery generates a current of 2 amp. How much solid iron is consumed in 1 hour?
2.08
How many moles of metallic aluminum (Al) could be produced from Al3+ at a current of 0.09 amperes for 964,853 seconds?
0.3 mol Al
Yes. We aren't given a balanced equation but we can say for sure that we need to convert Al3+ into Al which would be this half-reaction:
3e– + Al3+ → Al (s)
So we know that for every mole of Al we make, we need 3 moles of electrons.
We are given a current (0.09 C/ 1 s) and an amount of time (964,853 s). There are many ways to set up this problem. Here's one way - a stoichiometry problem:
What current is required to produce 91.6 g of chromium metal from chromium (VI) oxide in 12.4 hours?
22.8 A
The standard potential of the cell
Pt (s) | Fe2+ (aq), Fe3+ (aq) || Ag+ (aq) | Ag (s)
is +0.029 V at 25oC.
Calculate ∆G˚ for the reaction:
Fe2+ (aq) + Ag+ ⇌ Fe3+ (aq) + Ag (s)
-2.8 kJ/mol rxn
Yes. In order to calculate ∆G˚ we need the total moles of electrons involved, "n", and the standard potential, "E". The standard potential is given (0.029 V).
In order to determine, "n" the total moles of electrons involved requires a look at the balanced reaction. Ag+ is reduced with one electron to Ag. Fe2+ is oxidized with one electron to Fe3+. So the moles of electrons used in this overall reaction is 1 mole e–. Thus n = 1 mole e– per mole reaction
∆G˚ = –nFE˚ = –(1mol e–/mol rxn)(96,485 C/mol e–)(0.029 V) = –2,798.065 J/mol rxn
∆G˚ = –2.8 kJ/mol rxn
If the standard free energy change for combustion of 1 mole of CH4 (g) is –818 kJ, calculate the standard voltage that could be obtained from a fuel cell using this reaction. Hint: First write out the combustion of 1 mole of CH4 (g). Then, write out the half-reactions from this overall reaction and balance assuming acidic conditions.
+1.06 V
Yes. To calculate E we need ∆G and n. ∆G is –818 kJ/mol CH4. To calculate n (moles of electrons), we write out the unbalanced combustion reaction of methane:
CH4 (g) + O2 (g) → CO2 (g) + H2O (l)
Balanced half-reactions:
Ox: CH4 (g) + 2H2O (l) → CO2 (g) + 8H+ (aq) + 8e–
Red: O2 (g) + 4H+ (aq) + 4e– → 2H2O (l)
To combine we have to multiply the reduction reaction by 2.
Ox: CH4 (g) + 2H2O (l) → CO2 (g) + 2H+ (aq) + 8e–
Red x 2: 2O2 (g) + 8H+ (aq) + 8e– → 4H2O (l)
Combine and eliminate like terms:
CH4 (g) + 2O2 (g) → CO2 (g) + 2H2O (l)
8 moles of electrons were transferred in the combustion of 1 mole of methane. Now we can calculate E˚:
∆G˚ = –nFE˚ = –818 kJ = –(8 mol e–)(96,485 C/mol e–)E˚
–818,000 J = –(8 mol e–)(96,485 C/mol e–)E˚
E˚ = +1.06 V
The equilibrium constant for the reaction
2Hg (l) + 2Cl– (aq) + 2Ni2+ (aq) → Ni (s) + Hg2Cl2 (s)
is 5.6 x 10–20 at 25oC. Without calculations, we know this reaction is _______________ at 25oC. With calculations, we know that the value of E˚ for a cell utilizing this reaction is __________
Non-Spontaneous ; -0.57 V
The standard potential of the cell
Pt (s) | Fe2+ (aq), Fe3+ (aq) || Ag+ (aq) | Ag (s)
is +0.029 V at 25°C. Without calculating anything, we know that _________________ at 25°C. The equilibrium constant for the reaction at 25° is _________________
Spontaneous ; 3.1
ΔG° less than 0 matches K _______________ 1, which matches E° 0 _____________ and they all mean that the process is "_________________" as written and the are ____________ favored.
ΔG° > 0 matches K _____________ 1, which matches E° _______________ 0 and they all mean that the process is "____________" as written and the are _______________ favored.
greater than, greater than, spontaneous, product
less than, less than, non-spontaneous, reactant favored
Calculate the Ksp of AgI at 25˚C given the following information:
reaction E° (V)
reduction: AgI(s) + e− ⇌ Ag(s) + I−(aq) –0.1517
V
oxidation: Ag(s) ⇌ Ag+(aq) + e− −0.7990 V
net reaction:
AgI(s) ⇌ Ag+(aq) + I−(aq) _____ V
8.5 x 10^-17