IMPROPER FRACTION
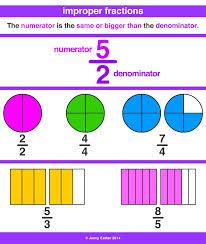
A fraction that shows an amount GREATER than one whole. The numerator is GREATER than the denominator. For example ⁷⁄₄ .
MIXED NUMBER
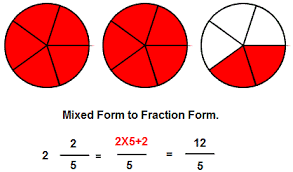
A number that has a WHOLE part AND a FRACTION part. For example 1 ⁴⁄₅ .
RATIO

A comparison of 2 or more quantities measured with the same unit. For example the number of girls to boys in the class is 6:9.
NUMERATOR
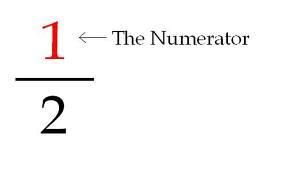
The part of a fraction that tells how many equal parts to count. The TOP number in a fraction. For example in ⅔, the numerator is 2.
DENOMINATOR
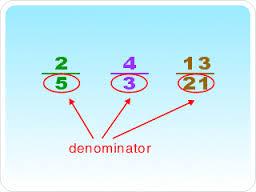
The part of a fraction that tells how many equal parts are in one whole. The denominator is the BOTTOM number in a fraction. For example ⅔, the denominator is 3. There are 3 parts in one whole.
ACUTE ANGLE
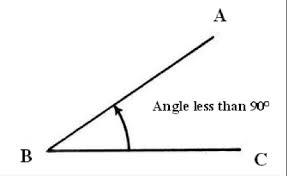
An angle that measures less than 90°.
OBTUSE ANGLE
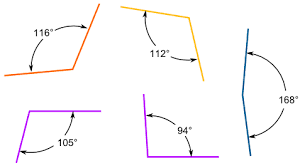
An angle that measures more than 90° but less than 180°.
REFLEX ANGLE
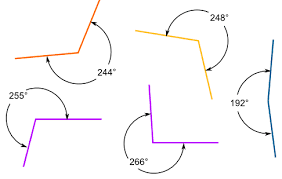
An angle that measures more than 180° and less than 360°.
ANGLE
Forms when 2 lines meet creating a vertex.
RIGHT ANGLE
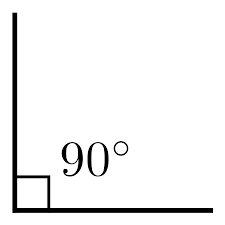
An angle that measures exactly 90° and usually indicated by a small square in the angle.
STRAIGHT ANGLE
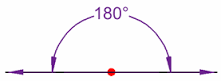
An angle that measures exactly 180°. It is a straight line.
VARIABLE

A letter that is used to represent a # in an equation or an expression.
3b=12(eq) 4x – 2(ex)
CONSTANT

In Algebra, a number on its own - a fixed number.
2t + 5
(5 is constantly a pain in the butt and is in a time out and can't play with anyone else)
NUMERICAL COEFFICIENT
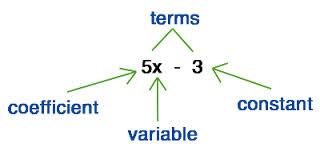
A number used to multiply a variable.
4n-2
4 is the term we are describing because it's madly in love with the variable. He's always attached to the variable...ALWAYS!
X AXIS
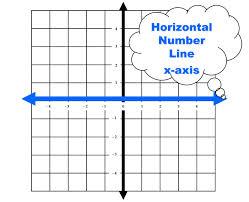
The line on a graph that runs horizontally (left-right) through zero.
OPERATION

A mathematical process.
The most common are add,
subtract, multiply and divide (+, -, ×, ÷ ).
Y AXIS
The line on a graph that runs vertically (up-down) through zero.
ORDERED PAIR

Two numbers written in a certain order in parentheses like
this: (4,5) or (x,y).
Used to show the position on a graph, where the
"x" (horizontal) value is first, and the "y"
(vertical) value is second.
Here the point (12,5)
is 12 units to the right, and 5 units up.
EQUIVALENT

Having the same value.
$1 = 100¢
120
seconds = 2 minutes
5n = 20
COMMON MULTIPLE

A number that is a multiple of 2 or more numbers.
6 is a common multiple of 2 and 3
PRIME NUMBER
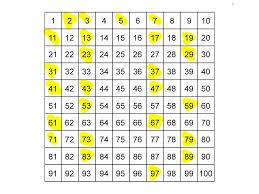
A number can be divided evenly only by 1 or itself
2, 3,
5, 7, 9, etc…
COMPOSITE NUMBER

A whole number that can be divided evenly by numbers other than 1 or itself. 9=1x9, 3x3
COMMON FACTOR

A number that is a factor of the given numbers: 3 is a common factor of 15, 9 and 21.
ORDER OF OPERATIONS
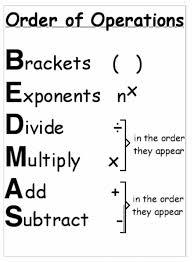
The rules of which calculation comes first in an expression. BEDMAS
INTEGER
A number that is either positive (+) or negative ( - ).
-23, -1, 5, 10, 97. The larger the NEGATIVE number the smaller it is. The larger the POSITIVE number, the bigger the number is.
POSITIVE INTEGER
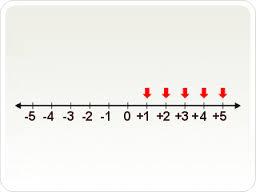
Zero is neither negative nor positive.)
5 is positive
five and it is found to the RIGHT of ZERO on the number line.
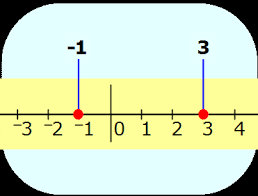
NEGATIVE INTEGER
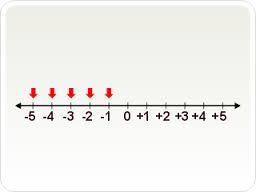
Less than zero and written with a minus sign in front of it: -5 is negative five and it is found to the LEFT of ZERO on the number line.
ZERO PAIR
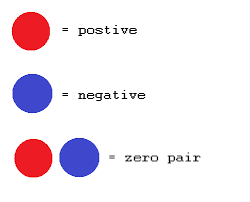
A pair of number with a positive and negative sign whose sum is zero. (+,-) For example: +2 and -2 .
OPPOSITE INTEGER

For each + integer, there is a - integer, and these integers are called opposites. For example, -3 is the opposite of 3.
EXPANDED FORM
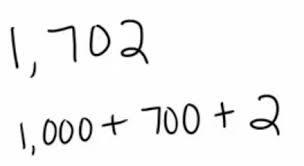
Writing a number to show the value of each digit.
It is shown as a sum of each digit
multiplied by its matching place value (units, tens, hundreds, etc.)
23 456 = 20000 + 3000 + 400 + 50 +6
STANDARD FORM

A general term meaning "written down in the way most commonly accepted" usually in numbers. For example: 56 347.
DEGREE
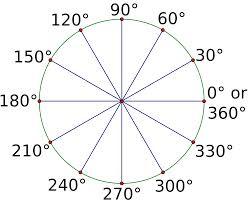
A measure for angles. There are 360 degrees in a full rotation (a circle). The symbol for degrees is °. Example: 90 degrees (90°) is a right angle.
TRIANGLE
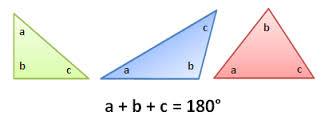
The sum of the interior angles of every triangle is equal to 180°.
QUADRILATERAL
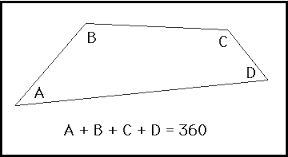
The sum of the interior angles of a quadrilateral is equal to 360°.
ISOSCELES TRIANGLE
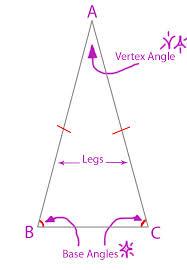
A triangle with two = sides, two = angles, and one = line of symmetry. The angles opposite the equal sides are also equal.
SCALENE TRIANGLE
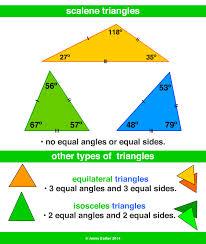
A triangle with all s ides and all angles of different lengths and degrees. There is no line of symmetry either.
RIGHT TRIANGLE
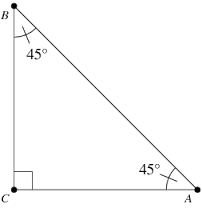
A triangle that has a right angle (90°).
OBTUSE TRIANGLE
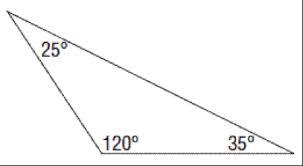
A triangle that has ONE angle greater than 90°.
PERIMETER
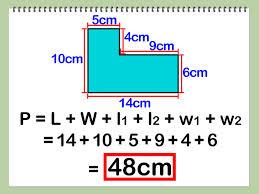
The distance around a two-dimensional shape.
Example: it is the total OUTSIDE of a shape
(add up every side).
IRREGULAR POLYGON
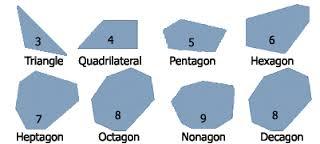
A polygon that does not have all sides equal and all angles equal. Even if ONE side is different, it is one of these.
REGULAR POLYGON
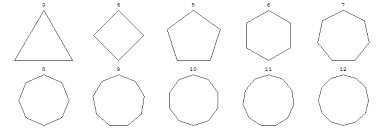
A shape where ALL angles and ALL sides are equal.
TRANSLATION
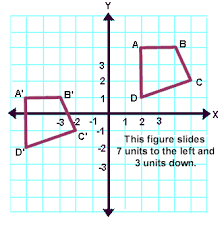
Moving a shape, without rotating or flipping it.
"Sliding". The shape still looks exactly the same, the shape is just in a different place.
ROTATION
A circular movement.
There is a central point that stays fixed
and everything else moves around
that point in a circle. In other words,
stick a NAIL in one corner and spin.
REFLECTION
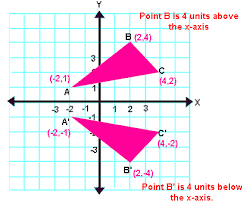
An image or shape as it would be seen in a mirror.
CONTINUOUS DATA
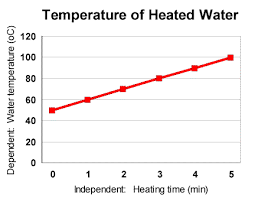
Data that can take any value (within a range)
Example:
People's heights could be any value (within the range of human
heights), not just certain fixed heights.
DISCRETE DATA
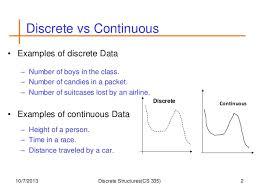
Data that can only take certain values.
For example: the
number of students in a class (you can't have half a student).
PROBABILITY
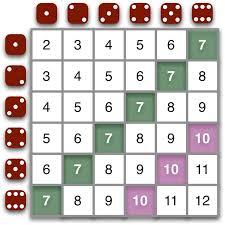
Probability is the chance that something will happen - how likely it is that some event will happen.
THEORETICAL PROBABILITY
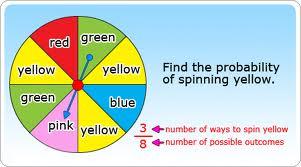
The likelihood that an outcome will happen.
In grade 6 terms, this is what is SUPPOSED to happen.
EXPERIMENTAL PROBABILITY
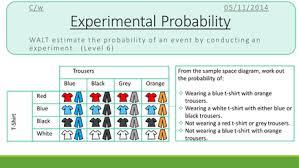
The likelihood that something occurs based on the RESULTS of the experiment. In grade 6 terms, this is EXACTLY what happens when you actually DO the experiment.
