(a) How many different 7-place license plates are possible if the first 2 places are for letters and the other 5 for numbers?
(b) Repeat part (a) under the assumption that no letter or number can be repeated in a single license plate.
(a)
Number of license plates:
26 x 26 x 10 x 10 x 10 x 10 x 10
= 67,600,000
(b)
Number of license plates with no repeated letters or digits:
26 x 25 x 10 x 9 x 8 x 7 x 6
= 19,656,00
How many outcome sequences are possible when a die is rolled four times, where we say, for instance, that the outcome is 3, 4, 3, 1 if the first roll landed on 3, the second on 4, the third on 3, and the fourth on 1?
Possible outcomes for 1 roll =
6 (1,2,3,4,5,6)
Possible outcomes for 4 rolls =
6 x 6 x 6 x 6 = 1296
Twenty workers are to be assigned to 20 different jobs, one to each job. How many different assignments are possible?
Number of permutations = 20!
John, Jim, Jay, and Jack have formed a band consisting of 4 instruments. If each of the boys can play all 4 instruments, how many different arrangements are possible? What if John and Jim can play all 4 instruments, but Jay and Jack can each play only piano and drums?
(a)
Total arrangements for 4 boys playing 4 instruments = 4! = 24
(b)
Total arrangements for Jay and Jack to be assigned piano and drums = 2!
Total arrangements for John and Jim to be assigned the other two instruments = 2!
Total arrangements = 2! x 2! = 4
For years, telephone area codes in the United States and Canada consisted of a sequence of three digits. The first digit was an integer between 2 and 9, the second digit was either 0 or 1, and the third digit was any integer from 1 to 9. How many area codes were possible? How many area codes starting with a 4 were possible?
(a)
1st digit = 2-9 (8 options)
2nd digit = 0-1 (2 options)
3rd digit = 1-9 (9 options)
Total possible area codes: 8 x 2 x 9 = 144
(b)
1st digit = 4 (1 option)
2nd digit = 0-1 (2 options)
3rd digit = 1-9 (9 options)
Total possible area codes: 1 x 2 x 9 = 18
A well-known nursery rhyme starts as follows:
“As I was going to St. Ives
I met a man with 7 wives.
Each wife had 7 sacks.
Each sack had 7 cats.
Each cat had 7 kittens. . .”
How many kittens did the traveler meet?
7 x 7 x 7 x 7 = 2401
(a) In how many ways can 3 boys and 3 girls sit in a row?
(b) In how many ways can 3 boys and 3 girls sit in a row if the boys and the girls are each to sit together?
(c) In how many ways if only the boys must sit together?
(d) In how many ways if no two people of the same sex are allowed to sit together?
(a)
Total ways: 6! = 720
(b)
3 boys can sit in 3! ways
3 girls can sit in 3! ways
2 groups of boys and girls can sit in 2! ways
Total ways: 3! x 3! x 2! = 72
(c)
3 girls can sit in 3! ways
Boys can sit in any of the remaining four positions (_G1_G2_G3_)
3 boys can also sit in 3! ways
Total ways: 3! x 4 x 3! = 144
(d)
2 ways (BGBGBG or GBGBGB)
3 girls can also sit in 3! ways
3 boys can also sit in 3! ways
Total ways: 2 x 3! x 3! = 72
How many different letter arrangements can be made from the letters
(a) Fluke?
(b) Propose?
(c) Mississippi?
(d) Arrange?
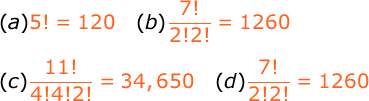
Notes for b, c and d:
Duplicate letters are taken into consideration
A child has 12 blocks, of which 6 are black, 4 are red, 1 is white, and 1 is blue. If the child puts the blocks in a line, how many arrangements are possible?
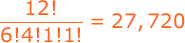
In how many ways can 8 people be seated in a row if:
(a) there are no restrictions on the seating arrangement?
(b) persons A and B must sit next to each other?
(c) there are 4 men and 4 women and no 2 men or 2 women can sit next to each other?
(d) there are 5 men and they must sit next to each other?
(e) there are 4 married couples and each couple must sit together?
(a)
8 people can be seated in 8! ways = 40,320
(b)
A and B can be seated in 2! ways
The remaining 7 can be seated in 7! ways
Total ways: 7! x 2! = 10,080
(c)
4 men can be seated in 4! ways
4 women can be seated in 4! ways
There are 2 ways to seat either MWMWMWMW or WMWMWMWM
Total ways: 4! x 4! x 2 = 1152
(d)
3 woman can be seated in 3! ways
Men can sit together in 4 places (1-5, 2-6, 3-7 or 4-8)
5 men can be seated in 5! ways
Total ways: 3! x 4 x 5! = 2880
(e)
4 couples can be seated in 4! ways
2 people part of a couple can be seated in 2! ways
Total ways: 4! x 2! x 2! x 2! x 2! = 384
In how many ways can 3 novels, 2 mathematics books, and 1 chemistry book be arranged on a bookshelf if:
(a) the books can be arranged in any order?
(b) the mathematics books must be together and the novels must be together?
(c) the novels must be together, but the other books can be arranged in any order?
(a)
Total ways: 6! = 720
(b)
3 novels can be arranged in 3! ways
2 mathematics books can be arranged in 2! ways
1 chemistry book can be arranged in 1! way
3 groups of books can be arranged in 3! ways
Total ways: 3! x 2! x 1! x 3! = 72
(c)
3 novels equal 1 group
4 groups can be arranged in 4! ways
3 novels can be arranged in 3! ways in a group
Total ways: 4! x 3! = 144
Five separate awards (best scholarship, best leadership qualities, and so on) are to be presented to selected students from a class of 30. How many different outcomes are possible if:
(a) a student can receive any number of awards?
(b) each student can receive at most 1 award?
(a)
30 x 30 x 30 x 30 x 30 = 24,300,000
(b)
30 students eligible for 1st award
29 students eligible for 2nd award
and so on...
30 x 29 x 28 x 27 x 26 = 17,100,720
Consider a group of 20 people. If everyone shakes hands with everyone else, how many handshakes take place?
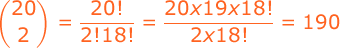
How many 5-card poker hands are there?
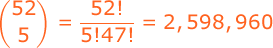
A dance class consists of 22 students, of which 10 are women and 12 are men. If 5 men and 5 women are to be chosen and then paired off, how many results are possible?
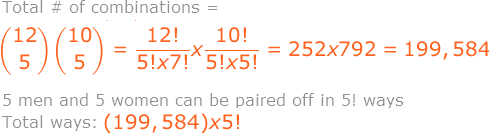
A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How many choices are possible if:
(a) both books are to be on the same subject?
(b) the books are to be on different subjects?
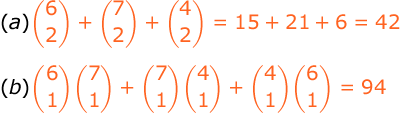
Notes for a:
Sells 2 math books = (6c2)
Sells 2 science books = (7c2)
Sells 2 economics books = (4c2)
Notes for b:
1 math book & 1 science book = (6c1)(7c1)
1 science book & 1 economics book = (7c1)(4c1)
1 economics book & 1 math book = (4c1)(6c1)
Seven different gifts are to be distributed among 10 children. How many distinct results are possible if no child is to receive more than one gift?
10 x 9 x 8 x 7 x 6 x 5 x 4
= 604,800 distinct gifts
A committee of 7, consisting of 2 Republicans, 2 Democrats, and 3 Independents, is to be chosen from a group of 5 Republicans, 6 Democrats, and 4 Independents. How many committees are possible?
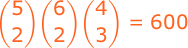
Notes:
# of ways to select 2 Republicans = (5c2)
# of ways to select 2 Democrats = (6c2)
# of ways to select 3 Independents = (4c3)
From a group of 8 women and 6 men, a committee consisting of 3 men and 3 women is to be formed. How many different committees are possible if:
(a) 2 of the men refuse to serve together?
(b) 2 of the women refuse to serve together?
(c) 1 man and 1 woman refuse to serve together?
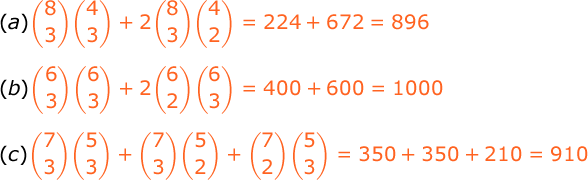
A person has 8 friends, of whom 5 will be invited to a party.
(a) How many choices are there if 2 of the friends are feuding and will not attend together?
(b) How many choices if 2 of the friends will only attend together?
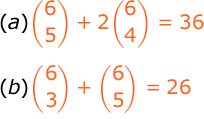
Notes for a:
# of ways if both fighting friends are not invited = (6c5)
# of ways if one of the fighting friend is invited = (6c4) x 2
Notes for b:
# of ways if they attend = (6c3)
# of ways if they do not attend = (6c5)
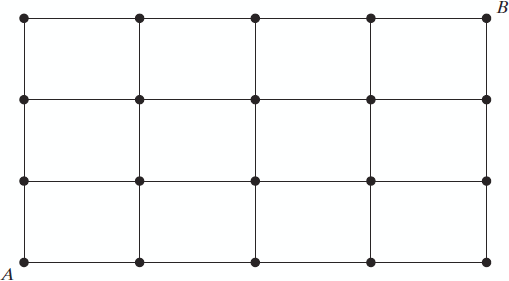
Consider the grid of points shown here. Suppose that, starting at the point labeled A, you can go one step up or one step to the right at each move. This procedure is continued until the point labeled B is reached. How many different paths from A to B are possible?
Hint: Note that to reach B from A, you must take 4 steps to the right and 3 steps upward.

Notes:
Answer shows the number of ways to select 4 steps to the right out of 7.
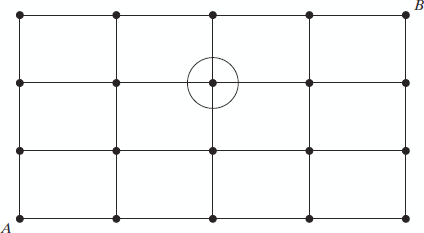
In Problem 21, how many different paths are there from A to B that go through the point circled in the following lattice?
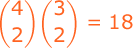
Notes:
To reach circled point for A, you need to take 2 steps up and 2 steps to the right. 2 steps to the right out of 4 total steps = (4c2)
To reach point B from circled point, you need to take 1 step up and 2 steps to the right. 2 steps to the right out of 3 total steps = (3c2)
A psychology laboratory conducting dream research contains 3 rooms, with 2 beds in each room. If 3 sets of identical twins are to be assigned to these 6 beds so that each set of twins sleeps in different beds in the same room, how many assignments are possible?
3 pair of twins into 3 different rooms = 3!
One bed for each twin in one room = 2! = 2
Total ways: 3! x 2 x 2 x 2 = 48
Expand (3x² + y)⁵
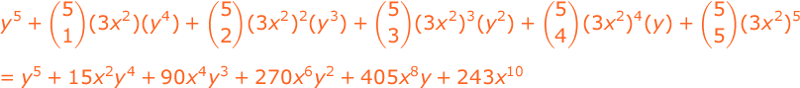
The game of bridge is played by 4 players, each of whom is dealt 13 cards. How many bridge deals are possible?

Expand (x₁ + 2x₂ + 3x₃)⁴
Good Luck :)
If 12 people are to be divided into 3 committees of respective sizes 3, 4, and 5, how many divisions are possible?
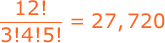
If 8 new teachers are to be divided among 4 schools, how many divisions are possible? What if each school must receive 2 teachers?
(a)
4⁸ = 65,536
(b)
8!/2!2!2!2! = 2520
Ten weight lifters are competing in a team weightlifting contest. Of the lifters, 3 are from the United States, 4 are from Russia, 2 are from China, and 1 is from Canada. If the scoring takes account of the countries that the lifters represent, but not their individual identities, how many different outcomes are possible from the point of view of scores? How many different outcomes correspond to results in which the United States has 1 competitor in the top three and 2 in the bottom three?
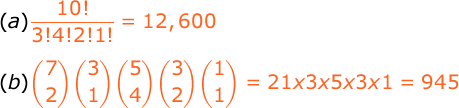
Notes for b:
selecting 2 out 7 and 1 out of 3 = (7c2)(3c1)
selecting next 4 positions out of 5 non-US members = (5c4)
selecting 2 positions out of 3 for US members = (3c2)
selecting 1 position out of 1 remaining non-US member = (1c1)
Delegates from 10 countries, including Russia, France, England, and the United States, are to be seated in a row. How many different seating arrangements are possible if the French and English delegates are to be seated next to each other and the Russian and U.S. delegates are not to be next to each other?
Calculate French and English next to each other:
French and English can be arranged in 2! ways
All 9 groups can be arranged in 9! ways
Totals ways: 2! x 9! = 725,760
Calculate Russian and US not next to each other:
All 8 groups can be arranged in 8! ways
The 2 groups French & English and Russian & US can be arranged 2! ways each
Totals ways: 8! x 2! x 2! = 161,280
To get answer need to subtract second from first:
(2! x 9!) - (8! x 2! x 2!) = 564,480
If 8 identical blackboards are to be divided among 4 schools, how many divisions are possible? How many if each school must receive at least 1 blackboard?
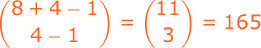
Notes:
n₁ + n₂ + n₃ + n₄ = 8
n is the # of blackboards for a particular school
An elevator starts at the basement with 8 people (not including the elevator operator) and discharges them all by the time it reaches the top floor, number 6. In how many ways could the operator have perceived the people leaving the elevator if all people look alike to him? What if the 8 people consisted of 5 men and 3 women and the operator could tell a man from a woman?
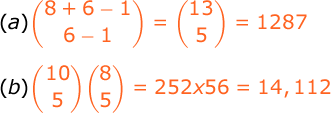
We have 20 thousand dollars that must be invested among 4 possible opportunities. Each investment must be integral in units of 1 thousand dollars, and there are minimal investments that need to be made if one is to invest in these opportunities. The minimal investments are 2, 2, 3, and 4 thousand
dollars. How many different investment strategies are available if:
(a) an investment must be made in each opportunity?
(b) investments must be made in at least 3 of the 4 opportunities?
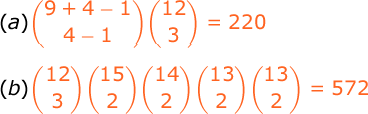
Notes for a:
n₁ + n₂ + n₃ + n₄ = 9
Notes for b:
investments made for all = (12c3)
investments (2,2,3) = (15c2)
investments (2,2,4) = (14c2)
investments (2,3,4) = (13c2)
investments (2,3,4) = (13c2)