Essentials of Statistics: Unit Test 2 Probabilty Flashcards

What is the probability of an event that is certain to occur?

A) 0.5
B) 0.95
C) 0.99
D) 1

What is the probability of an impossible event?

A) 1
B) 0.1
C) -1
D) 0

Which of the following cannot be a probability?

A) 2/3
B) 5/3
C) 3/5
D) 1/2

On a multiple choice test with four possible answers for each question, what is the probability of answering a question correctly if you make a random guess?

A) 1/4
B) 1
C) 3/4
D) 1/2

A bag contains 6 red marbles, 3 blue marbles, and 5 green marbles. If a marble is randomly selected
from the bag, what is the probability that it is blue?

A) 1/11
B) 1/3
C) 3/14
D) 1/5

Two 6-sided dice are rolled. What is the probability that the sum of the two numbers on the dice will be 5?

A) 8/9
B) 5/6
C) 1/9
D) 4

A class consists of 67 women and 12 men. If a student is randomly selected, what is the probability that the student is a woman?

A) 1/79
B) 12/79
C) 67/12
D) 67/79

In a certain class of students, there are 12 boys from Wilmette, 3 girls from Kenilworth, 9 girls from Wilmette, 6 boys from Glencoe, 2 boys from Kenilworth and 6 girls from Glencoe. If the teacher calls upon a student to answer a question, what is the probability that the student will be from Kenilworth?

A) 0.132
B) 0.079
C) 0.172
D) 0.1

Find the indicated complement.
Based on meteorological records, the probability that it will snow in a certain town on January 1st is 0.148. Find the probability that in a given year it will not snow on January 1st in that town.

A) 0.852
B) 6.757
C) 0.174
D) 1.148

Find the indicated probability.
A spinner has equal regions numbered 1 through 15.What is the probability that the spinner will stop on an even number or a multiple of 3?

A) 2/3
B) 1/2
C) 7/9
D) 1/3

If you pick a card at random from a well shuffled deck, what is the probability that you get a face card or a spade?

A) 11/26
B) 9/26
C) 1/22
D) 25/52

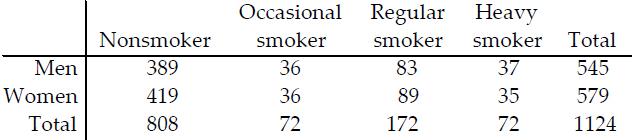
The table describes the smoking habits of a group of asthma sufferers.

If one of the 1124 people is randomly selected, find the probability that the person is a man or a heavy smoker.

A) 0.483
B) 0.516
C) 0.549
D) 0.514

Of the 73 people who answered "yes" to a question, 14 were male. Of the 53 people that answered "no" to the question, 9 were male. If one person is selected at random from the group, what is the probability that the person answered "yes" or was male?

A) 0.192
B) 0.183
C) 0.651
D) 0.762

A 6-sided die is rolled. Find P(3 or 5).

A) 1/36
B) 1/6
C) 1/3
D) 2

A bag contains 6 red marbles, 2 blue marbles, and 1 green marble. Find P(not blue).

A) 7
B) 2/9
C) 7/9
D) 9/7

Find the probability of correctly answering the first 2 questions on a multiple choice test if random guesses are made and each question has 5 possible answers.

A) 1/32
B) 5/2
C) 1/25
D) 2/5

A manufacturing process has a 70% yield, meaning that 70% of the products are acceptable and 30% are defective. If three of the products are randomly selected, find the probability that all of them are acceptable.

A) 0.027
B) 2.1
C) 0.343
D) 0.429

A bin contains 60 light bulbs of which 5 are defective. If 4 light bulbs are randomly selected from the bin with replacement, find the probability that all the bulbs selected are good ones. Round to the nearest thousandth if necessary.

A) 0.917
B) 0.706
C) 0.726
D) 0

When a pair of dice are rolled there are 36 different possible outcomes: 1-1, 1-2, ... 6-6. If a pair of dice are rolled 5 times, what is the probability of getting a sum of 5 every time? Round to eight decimal places.

A) 0.00032
B) 0.04
C) 0.00001694
D) 0.00005168

In a homicide case 7 different witnesses picked the same man from a line up. The line up contained 5 men. If the identifications were made by random guesses, find the probability that all 7 witnesses would pick the same person.

A) 0.0000595
B) 1.4
C) 0.0000128
D) 0.000064

You are dealt two cards successively (without replacement) from a shuffled deck of 52 playing cards. Find the probability that both cards are black. Express your answer as a simplified fraction.

A) 1/2652
B) 13/51
C) 25/102
D) 25/51

You are dealt two cards successively (without replacement) from a shuffled deck of 52 playing cards. Find the probability that the first card is a King and the second card is a queen. Express your answer as a simplified fraction.

A) 2/13
B) 1/663
C) 13/102
D) 4/663

What is the probability that 4 randomly selected people all have different birthdays? Round to four decimal places.

A) 0.9836
B) 0.9891
C) 0.9918
D) 0.9729

A IRS auditor randomly selects 3 tax returns from 55 returns of which 6 contain errors.What is the probability that she selects none of those containing errors? Round to four decimal places.

A) 0.7071
B) 0.0013
C) 0.7023
D) 0.0008

Provide a written description of the complement of the given event.

When 100 engines are shipped, all of them are free of defects.

A) None of the engines are defective.
B) At most one of the engines is defective.
C) All of the engines are defective.
D) At least one of the engines is defective.

Provide a written description of the complement of the given event.

When several textbooks are edited, none of them are found to be free of errors.

A) All of the textbooks are free of errors.
B) One of the textbooks is free of errors.
C) At most one of the textbooks is free of errors.
D) At least one of the textbooks is free of errors.

Find the indicated probability. Round to the nearest thousandth.

An unprepared student makes random guesses for the ten true-false questions on a quiz. Find the
probability that there is at least one correct answer.

A) 0.999
B) 0.100
C) 0.900
D) 0.001

Find the indicated probability. Round to the nearest thousandth.

A sample of 4 different calculators are randomly selected from a group containing 18 that are defective and 37 that have no defects. What is the probability that at least one of the calculators is defective?

A) 0.806
B) 0.795
C) 0.180
D) 0.194

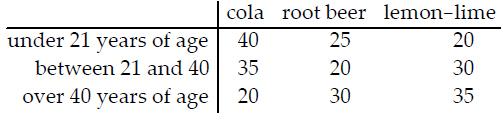
Find the indicated probability.
The table shows the soft drinks preferences of people in three age groups.

If one of the 255 subjects is randomly selected, find the probability that the person is over 40 years of age given that they drink root beer.

A) 5/17
B) 6/17
C) 2/5
D) None of the above is correct.

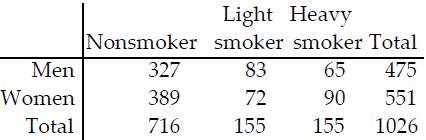
The table describes the smoking habits of a group of asthma sufferers.

If one of the 1026 subjects is randomly selected, find the probability that the person chosen is a nonsmoker given that it is a woman. Round to the nearest thousandth.

A) 0.543
B) 0.379
C) 0.706
D) 0.437

There are 13 members on a board of directors. If they must form a subcommittee of 5 members, how many different subcommittees are possible?

A) 120
B) 371,293
C) 1287
D) 154,440

The library is to be given 7 books as a gift. The books will be selected from a list of 16 titles. If each book selected must have a different title, how many possible selections are there?

A) 57,657,600
B) 11,440
C) 112
D) 268,435,456

The organizer of a television show must select 5 people to participate in the show. The participants will be selected from a list of 24 people who have written in to the show. If the participants are selected randomly, what is the probability that the 5 youngest people will be selected?

A) 1/5100480
B) 1/120
C) 1/42,504
D) 1/3

How many 3-digit numbers can be formed using the digits 1, 2, 3, 4, 5, 6, 7 if repetition of digits is not allowed?

A) 210
B) 6
C) 5
D) 343

How many ways can 6 people be chosen and arranged in a straight line if there are 8 people to choose from?

A) 20,160
B) 40,320
C) 720
D) 48

There are 9 members on a board of directors. If they must elect a chairperson, a secretary, and a treasurer, how many different slates of candidates are possible?

A) 729
B) 84
C) 504
D) 362,880

A tourist in France wants to visit 5 different cities. If the route is randomly selected, what is the probability that she will visit the cities in alphabetical order?

A) 120
B) 1/5
C) 1/25
D) 1/120

The number of oil spills occurring off the Alaskan coast

A) Continuous
B) Discrete

The braking time of a car

A) Continuous
B) Discrete

Find the mean of the given probability distribution.

A) μ = 2.53
B) μ = 2.43
C) μ = 2.39
D) μ = 2.29

Find the mean of the given probability distribution.

The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.5729, 0.3424, 0.0767, 0.0076, and 0.0003, respectively. Round answer to the nearest hundredth.

A) μ = 0.42
B) μ = 0.52
C) μ = 2.00
D) μ = 1.09

Find the standard deviation for the given probability distribution.

A) σ = 1.45
B) σ = 1.41
C) σ = 2.91
D) σ = 1.99

A police department reports that the probabilities that 0, 1, 2, and 3 burglaries will be reported in a given day are 0.49, 0.38, 0.10, and 0.03, respectively. Find the standard deviation for the probability distribution. Round answer to the nearest hundredth.

A) σ = 1.04
B) σ = 0.78
C) σ = 0.60
D) σ = 1.02

Focus groups of 11 people are randomly selected to discuss products of the Famous Company. It is determined that the mean number (per group) who recognize the Famous brand name is 6.2, and the standard deviation is 0.51. Would it be unusual to randomly select 11 people and find that greater than 9 recognize the Famous brand name?

A) Yes
B) No

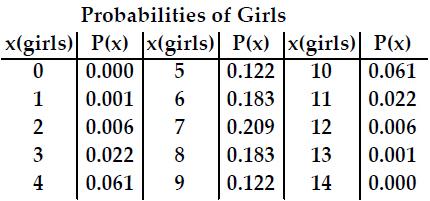
Assume that a researcher randomly selects 14 newborn babies and counts the number of girls selected, x. The probabilities corresponding to the 14 possible values of x are summarized in the given table. Answer the question using the table.

Find the probability of selecting exactly 8 girls.

A) 0.122
B) 0.000
C) 0.183
D) 0.022

Assume that a researcher randomly selects 14 newborn babies and counts the number of girls selected, x. The probabilities corresponding to the 14 possible values of x are summarized in the given table. Answer the question using the table.

Find the probability of selecting 12 or more girls.

A) 0.006
B) 0.022
C) 0.007
D) 0.001

A contractor is considering a sale that promises a profit of $20,000 with a probability of 0.7 or a loss (due to bad weather, strikes, and such) of $14,000 with a probability of 0.3. What is the expected profit?

A) $9800
B) $6000
C) $14,000
D) $23,800

Suppose you pay $2.00 to roll a fair die with the understanding that you will get back $4.00 for rolling a 2 or a 4, nothing otherwise. What is your expected value?

A) -$2.00
B) $4.00
C) -$0.67
D) $2.00

Suppose you buy 1 ticket for $1 out of a lottery of 1,000 tickets where the prize for the one winning ticket is to be $500.What is your expected value?

A) $0.00
B) -$0.40
C) -$1.00
D) -$0.50

A 28-year-old man pays $200 for a one-year life insurance policy with coverage of $120,000. If the probability that he will live through the year is 0.9994, what is the expected value for the insurance policy?

A) -$128.00
B) -$199.88
C) $119,928.00
D) $72.00

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.

Choosing 7 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green) one at a time without replacement, keeping track of the number of red marbles chosen.

A) Procedure results in a binomial distribution.
B) Not binomial: the trials are not independent.
C) Not binomial: there are more than two outcomes for each trial.
D) Not binomial: there are too many trials.

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.

Choosing 6 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green) one at a time with replacement, keeping track of the number of red marbles chosen.

A) Procedure results in a binomial distribution.
B) Not binomial: the trials are not independent.
C) Not binomial: there are more than two outcomes for each trial.
D) Not binomial: there are too many trials.

A test consists of 10 true/false questions. To pass the test a student must answer at least 6 questions correctly. If a student guesses on each question, what is the probability that the student will pass the test?

A) 0.172
B) 0.828
C) 0.205
D) 0.377

Find the probability of at least 2 girls in 10 births. Assume that male and female births are equally likely and that the births are independent events.

A) 0.945
B) 0.989
C) 0.044
D) 0.011

An airline estimates that 90% of people booked on their flights actually show up. If the airline books 71 people on a flight for which the maximum number is 69, what is the probability that the number of people who show up will exceed the capacity of the plane?

A) 0.005
B) 0.004
C) 0.001
D) 0.022

A company purchases shipments of machine components and uses this acceptance sampling plan: Randomly select and test 30 components and accept the whole batch if there are fewer than 3 defectives. If a particular shipment of thousands of components actually has a 6% rate of defects, what is the probability that this whole shipment will be accepted?

A) 0.165
B) 0.576
C) 0.277
D) 0.732

A multiple choice test has 10 questions each of which has 5 possible answers, only one of which is correct. If Judy, who forgot to study for the test, guesses on all questions, what is the probability that she will answer exactly 3 questions correctly?

A) 0.302
B) 0.799
C) 0.201
D) 0.00800

Suppose that 11% of people are left handed. If 5 people are selected at random, what is the probability that exactly 2 of them are left handed?

A) 0.0121
B) 0.0853
C) 0.0105
D) 0.171

The probability is 0.6 that a person shopping at a certain store will spend less than $20. For groups of size 24, find the mean number who spend less than $20.

A) 8.0
B) 14.4
C) 12.0
D) 9.6

A company manufactures batteries in batches of 26 and there is a 3% rate of defects. Find the mean number of defects per batch.

A) 7.8
B) 0.8
C) 78
D) 25.2

A company manufactures batteries in batches of 26 and there is a 3% rate of defects. Find the standard deviation for the number of defects per batch.

A) 0.6
B) 75.7
C) 0.8
D) 0.9

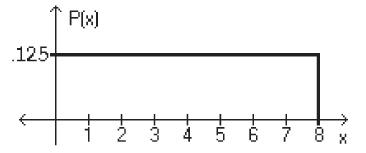
What is the probability that the random variable has a value greater than 4?

A) 0.500
B) 0.375
C) 0.450
D) 0.625

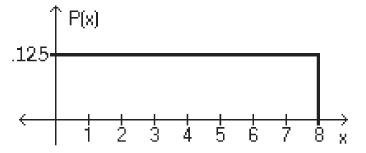
What is the probability that the random variable has a value less than 7.4?

A) 0.6750
B) 1.0500
C) 0.9250
D) 0.8000

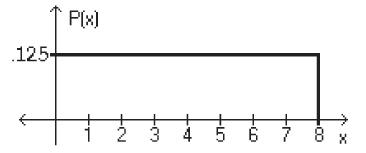
What is the probability that the random variable has a value between 0.1 and 6.2?

A) 0.8875
B) 0.7625
C) 1.0125
D) 0.6375

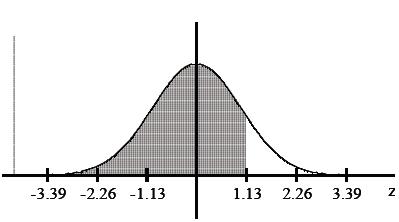
Find the area of the shaded region. The graph depicts the standard normal distribution with mean 0 and standard deviation 1.

A) 0.8485
B) 0.1292
C) 0.8708
D) 0.8907

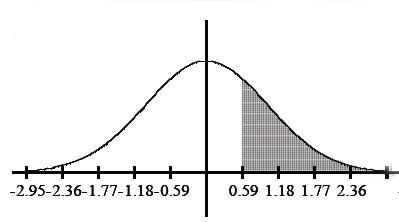
Find the area of the shaded region. The graph depicts the standard normal distribution with mean 0 and standard deviation 1.

A) 0.7224
B) 0.2224
C) 0.2776
D) 0.2190

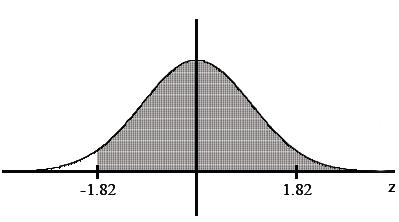
Find the area of the shaded region. The graph depicts the standard normal distribution with mean 0 and standard deviation 1.

A) -0.0344
B) 0.0344
C) 0.4656
D) 0.9656

If z is a standard normal variable, find the probability.

P(z > 0.59)

A) 0.7224
B) 0.2776
C) 0.2224
D) 0.2190

If z is a standard normal variable, find the probability.

P(z < 0.97)

A) 0.8315
B) 0.8078
C) 0.8340
D) 0.1660

If z is a standard normal variable, find the probability.

P(-0.73 < z < 2.27)

A) 1.54
B) 0.2211
C) 0.4884
D) 0.7557

z0.05

A) 1.545
B) 1.755
C) 1.645
D) 1.325

Assume that adults have IQ scores that are normally distributed with a mean of 100 and a standard deviation of 15 (as on theWechsler test). Find the probability that a randomly selected adult has an IQ between 90 and 120 (somewhere in the range of normal to bright normal).

A) 0.6014
B) 0.6568
C) 0.6227
D) 0.6977

Find P40, which is the IQ score separating the bottom40% from the top 60%.

A) 96.1
B) 95.2
C) 95.6
D) 96.2

Find the IQ score separating the top 14% from the others.

A) 83.7
B) 104.7
C) 116.2
D) 99.8

The amount of rainfall in January in a certain city is normally distributed with a mean of 3.4 inches and a standard deviation of 0.3 inches. Find the value of the quartile Q1.

A) 0.9
B) 3.2
C) 3.6
D) 3.3

Assume that women have heights that are normally distributed with a mean of 63.6 inches and a standard deviation of 2.5 inches. Find the value of the quartile Q3.

A) 66.1 inches
B) 67.8 inches
C) 64.3 inches
D) 65.3 inches

Assume that X has a normal distribution, and find the indicated probability.

The mean is μ = 137.0 and the standard deviation is σ = 5.3.

Find the probability that X is between 134.4 and 140.1.

A) 0.4069
B) 0.6242
C) 0.8138
D) 1.0311

The diameters of pencils produced by a certain machine are normally distributed with a mean of 0.30 inches and a standard deviation of 0.01 inches.What is the probability that the diameter of a randomly selected pencil will be less than 0.285 inches?

A) 0.0596
B) 0.4332
C) 0.0668
D) 0.9332

A bank's loan officer rates applicants for credit. The ratings are normally distributed with a mean of 200 and a standard deviation of 50. If an applicant is randomly selected, find the probability of a rating that is between 200 and 275.

A) 0.5
B) 0.4332
C) 0.9332
D) 0.0668

The lengths of human pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. What is the probability that a pregnancy lasts at least 300 days?

A) 0.4834
B) 0.0166
C) 0.9834
D) 0.0179

The scores on a certain test are normally distributed with a mean score of 60 and a standard deviation of 2.What is the probability that a sample of 90 students will have a mean score of at least 60.2108?

A) 0.1587
B) 0.3174
C) 0.8413
D) 0.3413

Assume that women's heights are normally distributed with a mean of 63.6 inches and a standard deviation of 2.5 inches. If 90 women are randomly selected, find the probability that they have a mean height between 62.9 inches and 64.0 inches.

A) 0.0424
B) 0.1739
C) 0.7248
D) 0.9318

Suppose that replacement times for washing machines are normally distributed with a mean of 9.3 years and a standard deviation of 1.1 years. Find the probability that 70 randomly selected washing machines will have a mean replacement time less than 9.1 years.

A) 0.4286
B) 0.0714
C) 0.4357
D) 0.0643

A final exam in Math 160 has a mean of 73 with standard deviation 7.8. If 24 students are randomly selected, find the probability that the mean of their test scores is greater than 78.

A) 0.0008
B) 0.8962
C) 0.0036
D) 0.0103

A final exam in Math 160 has a mean of 73 with standard deviation 7.8. If 24 students are randomly selected, find the probability that the mean of their test scores is less than 76.

A) 0.0301
B) 0.9699
C) 0.8962
D) 0.9203

The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability.

The probability of at least 42 boys

A) The area to the right of 42.5
B) The area to the right of 42
C) The area to the right of 41.5
D) The area to the left of 41.5

The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability.

The probability that the number of correct answers is between 22 and 48 inclusive

A) The area between 22.5 and 47.5
B) The area between 22 and 48
C) The area between 21.5 and 48.5
D) The area between 21.5 and 47.5

Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.

A certain question on a test is answered correctly by 22% of the respondents. Estimate the probability that among the next 150 responses there will be at most 40 correct answers.

A) 0.0694
B) 0.1003
C) 0.8997
D) 0.9306

Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.

Two percent of hair dryers produced in a certain plant are defective. Estimate the probability that of 10,000 randomly selected hair dryers, exactly 225 are defective.

A) 0.0057
B) 0.0034
C) 0.0051
D) 0.0065

Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.

Two percent of hair dryers produced in a certain plant are defective. Estimate the probability that of 10,000 randomly selected hair dryers, at least 219 are defective.

A) 0.0934
B) 0.9066
C) 0.0823
D) 0.0869