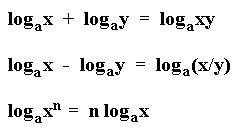sin(theta/2)
sin(theta/2)= +- root 1-cos(theta) divided by 2
cos(theta/2)
cos(theta/2)= +- root 1+cos(theta) divided by 2
sin (2theta)
sin(2theta) = 2sin(theta)cos(theta)
cos (2theta) #1
cos(2theta)=cos^2(theta)-sin^2(theta)
sin (a+b)
sin(a)cos(b)+cos(a)sin(b)
sin (a-b)
sin(a)cos(b)-cos(a)sin(b)
Cos(a+b)
cos(a+b)= cos(a)cos(b)-sin(a)sin(b)
Cos(a-b)
cos(a+b)= cos(a)cos(b)+sin(a)sin(b)
tan(a+b)
tan(a)+tan(b)/1-tan(a)tan(b)
tan(a-b)
tan(a)-tan(b)/1+tan(a)tan(b)
cos(2theta) #2
cos(2theta) = 1-2sin^2(theta)
cos(2theta)
cos(2theta) = 2cos^2-1
tan(2theta)
2tan(theta) = 2tan(theta)/1-tan^2(theta)
tan(a/2) #2
sin(theta)/cos(theta)+1
tan(a/2) #3
1-cos(theta)/sin(theta)
What is an even function?
A function that stays the same even when f(x)=f(-x)
What is an odd function?
A function where -f(x)=f(-x)
What are the three Pythagorean identities?
- sin²(θ) + cos²(θ) = 1: This is the most basic identity, representing the relationship between sine and cosine on the unit circle (x² + y² = r², with r=1).
- 1 + tan²(θ) = sec²(θ): Derived by dividing the first identity by cos²(θ).
- 1 + cot²(θ) = csc²(θ): Derived by dividing the first identity by sin²(θ).
What is the law of sines?
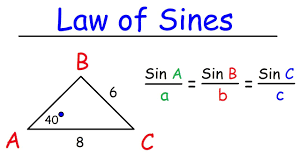
What is the law of cosines?
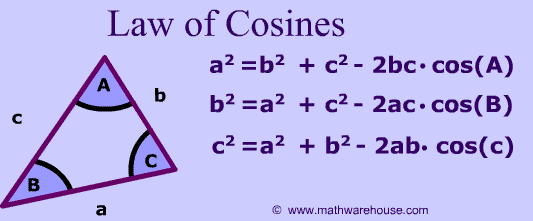
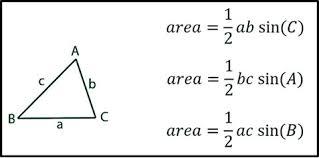
What is the Sin area formula?
What is Heron's Law?
What is the log change of base formula?
What are the three log properties?
