
Screen Reader Note: To calculate percent error, find the absolute value of the difference between experimental value and known value. Take this and divide it the known value. After that, multiply by 100 %. End of note.
Given the known heat of vaporization (delta H vap) of water is 44.01 kJ/mole, find the percent error using the experimentally determined delta H vap of 43.97 kJ/mole. Express with units of % in the units box.
Percent error = (|43.97 kJ/mole - 44.01 kJ/mole| x 100%) / 44.01 kJ/mole = 0.09089 % -> 0.091 %
An unknown liquid has a heat of vaporization of 34.13 kJ/mole. If the normal boiling point is 82, what is vapor pressure (in torr) of this liquid at room temperature of 25 degrees C? HINT: Normal boiling point occurs when the vapor pressure of the liquid is the same as atmospheric pressure (1 atm or 760 mm Hg).
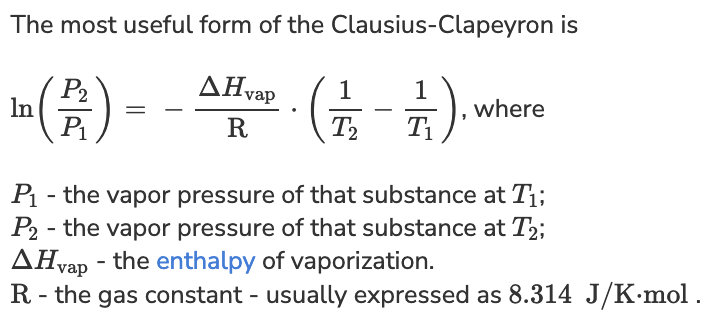
P1 = 760 torr
P2 = ?
T1 = 82 degrees C + 273 = 355 K
T2 = 25 degrees C + 273 = 298 K
delta H = 34.13 kJ/mole x (1000 J / 1 kJ) = 34,130 J/mole
R = 8.314 K/J/mole
ln (P2 / P1) = - (delta H / R) x (1/T2 - 1/T1)
P2 = P1 e[-(delta H / R) x (1/T2 - 1/T1)]
P2 = 760 torr e[-( 34,130 J/mole / 8.314 K/J/mole) x (1/298 K - 1/355 K)]
P2 = 83 torr
Ex.
In a calculator, input:
(760)e^((-34130/8.314)(1/298-1/355))
An unknown liquid has a heat of vaporization of 7.50 kJ/mole. If the vapor pressure of this liquid at -170 degrees C is 83 torr, what is the normal boiling point of this liquid in degrees C? HINT: Normal boiling point occurs when the vapor pressure of the liquid is the same as atmospheric pressure (1 atm or 760 mm Hg).
P1 = 760 torr
P2 = 83 torr
T1 = ?
T2 = -170 degrees C + 273 = 103 K
delta H = 7.50 kJ/mole x (1000 J / 1 kJ) = 7,500 J/mole
R = 8.314 K/J/mole
ln (P2 / P1) = - (delta H / R) x (1/T2 - 1/T1)
ln (83 torr / 760 torr) = - (7,500 J/mole / 8.314 K/J/mole) x (1/103 K - 1/T1)
T1 = 137.85658472 K
T1 = 137.85658472 K - 273.15 K = -135.29
T1 = -135 degrees C
Ex.
- Maybe can use (?): T2 = [ 1/T1 - (( R x ln(P2/P1) / delta H)) ]-1

Screen Reader Note: To calculate percent error, find the absolute value of the difference between experimental value and known value. Take this and divide it the known value. After that, multiply by 100 %. End of note.
Given the known heat of vaporization (delta H vap) of water is 44.01 kJ/mole, find the percent error using the experimentally determined delta H vap of 47.04 kJ/mole. Express with units of % in the units box.
Percent error = (|47.04 kJ/mole - 44.01 kJ/mole| x 100%) / 44.01 kJ/mole = 6.8847989 % -> 6.9 %
An unknown liquid has a heat of vaporization of 39.15 kJ/mole. If the normal boiling point is 85, what is vapor pressure (in torr) of this liquid at room temperature of 25 degrees C? HINT: Normal boiling point occurs when the vapor pressure of the liquid is the same as atmospheric pressure (1 atm or 760 mm Hg).
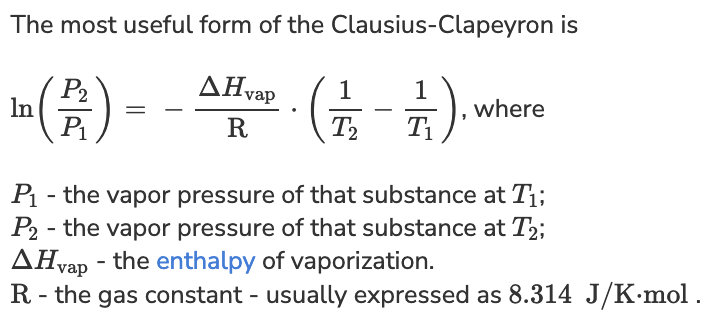
P1 = 760 torr
P2 = ?
T1 = 85 degrees C + 273 = 358 K
T2 = 25 degrees C + 273 = 298 K
delta H = 39.15 kJ/mole x (1000 J / 1 kJ) = 39,150 J/mole
R = 8.314 K/J/mole
ln (P2 / P1) = - (delta H / R) x (1/T2 - 1/T1)
P2 = P1 e[-(delta H / R) x (1/T2 - 1/T1)]
P2 = 760 torr e[-( 39,150 J/mole / 8.314 K/J/mole) x (1/298 K - 1/358 K)]
P2 = 53.784 torr
P2 = 54 torr
Ex.
In a calculator, input:
(760)e^((-39,150/8.314)(1/298-1/358))
An unknown liquid has a heat of vaporization of 5.50 kJ/mole. If the vapor pressure of this liquid at -170 degrees C is 111 torr, what is the normal boiling point of this liquid in degrees C? HINT: Normal boiling point occurs when the vapor pressure of the liquid is the same as atmospheric pressure (1 atm or 760 mm Hg).
P1 = 760 torr
P2 = 111 torr
T1 = ?
T2 = -170 degrees C + 273 = 103 K
delta H = 5.50 kJ/mole x (1000 J / 1 kJ) = 5,500 J/mole
R = 8.314 K/J/mole
ln (P2 / P1) = - (delta H / R) x (1/T2 - 1/T1)
ln (111 torr / 760 torr) = - (5,500 J/mole / 8.314 K/J/mole) x (1/103 K - 1/T1)
T1 = 147.04434362 K
T1 = 147.04434362 K - 273.15 K = -126.10565638
T1 = -126 degrees C