8B.2 In what ways does the quantum mechanical description of a harmonic oscillator merge with its classical description at high quantum numbers?
The correspondence principle (mentioned in Topic 8A.2(b)) states that
in the limit of very large quantum numbers quantum mechanics merges
with classical mechanics. The harmonic oscillator provides an example.
A classical harmonic oscillator’s range of motion is restricted by
classical turning points, which are determined by the oscillator’s
total energy; that energy can take on any real positive value. By
contrast, a quantum harmonic oscillator can tunnel past classical
turning points into the classically forbidden region with
a
non-zero probability. The total energy of a quantum harmonic
oscillator is quantized; not every real positive value is allowed. At
high quantum numbers, the probability of tunneling
beyond the
classical turning points falls (approaching the zero probability of
classical harmonic oscillators). Furthermore, the most likely place to
find the oscillator is near the classical turning points. (This is
true of the classical oscillator as well: because the speed
of
the oscillator vanishes at the turning points, the oscillator
spends more time near the turning points than elsewhere in its range.)
See Figure 8B.7 of the main text, particularly for v = 18,
to see
the probability distribution for large v approach the classical
picture. Finally, although the spacing between discrete allowed energy
levels is the same size at large quantum numbers as at small ones,
that spacing is a smaller fraction of total energy at large quantum
numbers; in that sense, the allowed energy levels are more nearly
continuous at
large quantum numbers than small.
8B.1(b) Calculate the zero-point energy of a harmonic oscillator consisting of a particle of mass 5.16 × 10−26 kg and force constant 285 N m−1.
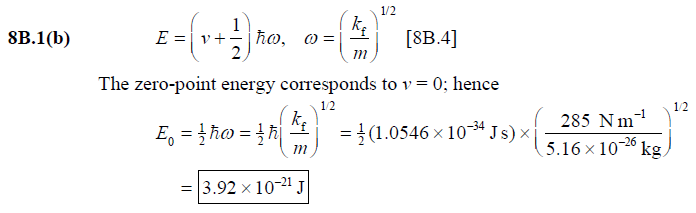
8B.2(b) For a certain harmonic oscillator of effective mass 2.88 ×
10−25 kg, the difference in adjacent energy levels is 3.17 zJ.
Calculate the force constant of
the oscillator.
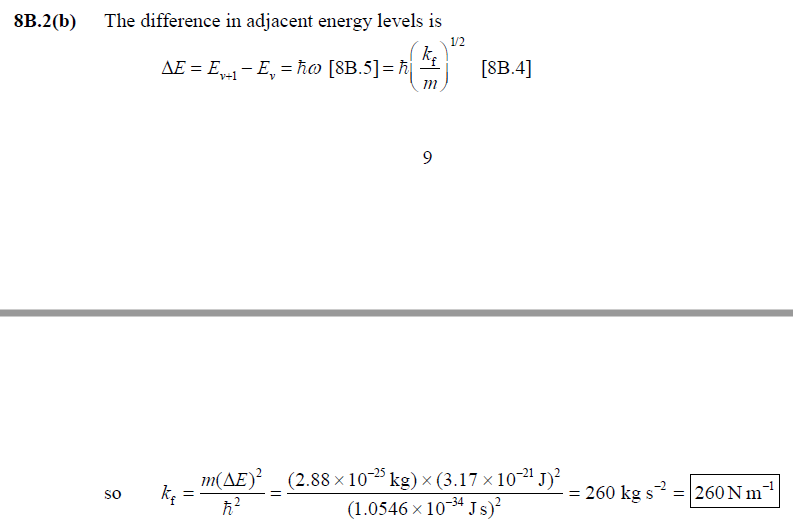

8B.6(b)
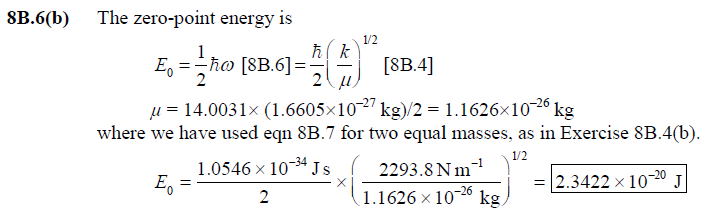
8B.7(b) Locate the nodes of the harmonic oscillator wavefunction with v = 5.

8B.8(b) What are the most probable displacements of a harmonic oscillator with v = 3?
