A mass m, attached to a horizontal massless spring with spring
constant k, is set into simple harmonic motion.
Its maximum
displacement from its equilibrium position is A. What is the mass’s
speed as it passes through its
equilibrium position?
(A) A √k/m
(B) A √m/k
(C) (1/A) √k/m
(D) (1/A) √m/k
(A)
A mass m is attached to a spring with a spring constant k. If the
mass is set into simple harmonic motion by a
displacement d from
its equilibrium position, what would be the speed, v, of the mass when
it returns to the
equilibrium position?
(A) v = √md/k
(B) v = √kd/m
(C) v = √kd/mg
(D) v = d√(k/m)
(D)
Which of the following is true for a system consisting of a mass
oscillating on the end of an ideal spring?
(A) The kinetic and
potential energies are equal to each other at all times.
(B) The
kinetic and potential energies are both constant.
(C) The maximum
potential energy is achieved when the mass passes through its
equilibrium position.
(D) The maximum kinetic energy and maximum
potential energy are equal, but occur at different times.
(D)
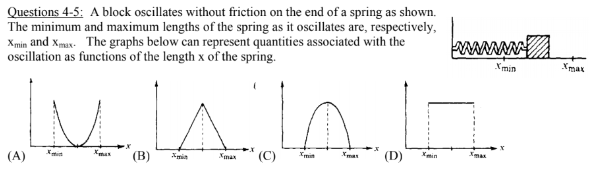
Which graph can represent the total mechanical energy of the
block-spring system as a function of x ?
(A) A
(B) B
(C) C
(D) D
(D) D

Which graph can represent the kinetic energy of the block as a
function of x ?
(A) A
(B) B
(C) C
(D) D
(C) C
An object swings on the end of a cord as a simple pendulum with
period T. Another object oscillates up and
down on the end of a
vertical spring also with period T. If the masses of both objects are
doubled, what are the
new values for the Periods?
Pendulum Mass on Spring
(A) T/ √2 T√ 2
(B) T T√ 2
(C) T√ 2 T
(D) T√ 2 T/ √2
(B)
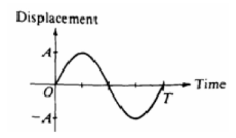
An object is attached to a spring and oscillates with amplitude
A
and period T, as represented on the graph. The nature of
the
velocity v and acceleration a of the object at time T/4 is
best
represented by which of the following?
(A) v > 0, a
> 0 (B) v > 0, a < 0
(C) v > 0, a = 0 (D) v = 0, a
< 0
(D)
When an object oscillating in simple harmonic motion is at its
maximum displacement from the equilibrium
position. Which of the
following is true of the values of its speed and the magnitude of the
restoring force?
Speed Restoring Force
(A) Zero
Maximum
(B) Zero Zero
(C) Maximum 1⁄2 maximum
(D)
Maximum Zero
(A)
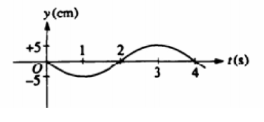
A particle oscillates up and down in simple harmonic motion.
Its
height y as a function of time t is shown in the diagram.
At what
time t does the particle achieve its maximum
positive
acceleration?
(A) 1 s (B) 2 s (C) 3 s (D) 4 s
(A)

The graph shown represents the potential energy U as a function of displacement x for an object on the end of a spring moving back and forth with amplitude x0. Which of the following graphs represents the kinetic energy K of the object as a function of displacement x ?
(D)
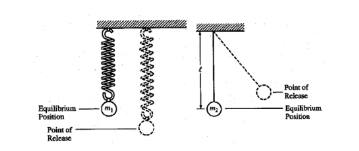
A sphere of mass m1, which is attached to a spring, is displaced
downward from its equilibrium position as shown
above left and
released from rest. A sphere of mass m2, which is suspended from a
string of length L, is displaced to
the right as shown above
right and released from rest so that it swings as a simple pendulum
with small amplitude.
Assume that both spheres undergo simple
harmonic motion
11. Which of the following is true for both spheres?
(A) The
maximum kinetic energy is attained as the sphere passes through its
equilibrium position
(B) The maximum kinetic energy is attained
as the sphere reaches its point of release.
(C) The minimum
gravitational potential energy is attained as the sphere passes
through its equilibrium position.
(D) The maximum gravitational
potential energy is attained when the sphere reaches its point of
release.
(E) The maximum total energy is attained only as the
sphere passes through its equilibrium position.
(A)

A sphere of mass m1, which is attached to a spring, is displaced
downward from its equilibrium position as shown
above left and
released from rest. A sphere of mass m2, which is suspended from a
string of length L, is displaced to
the right as shown above
right and released from rest so that it swings as a simple pendulum
with small amplitude.
Assume that both spheres undergo simple
harmonic motion
If both spheres have the same period of oscillation, which of the
following is an expression for the spring
constant
(A) L /
m1g
(B) g / m2L
(C) m2g / L
(D) m1g / L
(D)
A simple pendulum and a mass hanging on a spring both have a period
of 1 s when set into small oscillatory
motion on Earth. They are
taken to Planet X, which has the same diameter as Earth but twice the
mass. Which of the
following statements is true about the periods
of the two objects on Planet X compared to their periods on
Earth?
(A) Both are shorter.
(B) Both are the same.
(C)
The period of the mass on the spring is shorter; that of the pendulum
is the same.
(D) The period of the pendulum is shorter; that of
the mass on the spring is the same
(D)
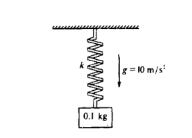
A 0.l -kilogram block is attached to an initially unstretched spring
of force constant k = 40 newtons per meter as
shown above. The
block is released from rest at time t = 0.
14. What is the amplitude, in meters, of the resulting simple harmonic motion of the block?
(A) (1/40)m
(B) (1/20)m
(C) (1/4)m
(D) (1/2)m
(A)

What will the resulting period of oscillation be?
(A) π/40
s
(B) π/20 s
(C) π/10 s
(D) π/4 s
C)
A ball is dropped from a height of 10 meters onto a hard surface so
that the collision at the surface may be
assumed elastic. Under
such conditions the motion of the ball is
(A) simple harmonic
with a period of about 1.4 s
(B) simple harmonic with a period of
about 2.8 s
(C) simple harmonic with an amplitude of 5 m
(D)
periodic with a period of about 2.8 s but not simple harmonic
(D)
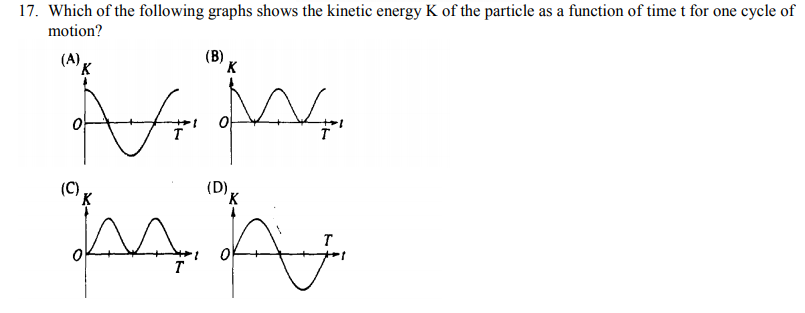
Which of the following graphs shows the kinetic energy K of the
particle as a function of time t for one cycle of
motion?
(B)
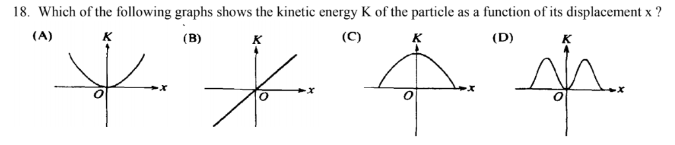
Which of the following graphs shows the kinetic energy K of the particle as a function of its displacement x ?
(C)
A mass m is attached to a vertical spring stretching it distance d.
Then, the mass is set oscillating on a spring
with an amplitude
of A, the period of oscillation is proportional to
A) √d/g
B) √g/d
C) √d/mg
D) √m2g/d
D)
Two objects of equal mass hang from independent springs of unequal
spring constant and oscillate up and down.
The spring of greater
spring constant must have the
(A) smaller amplitude of oscillation
(B) larger amplitude of oscillation
(C) shorter period of oscillation
(D) longer period of oscillation
(C)
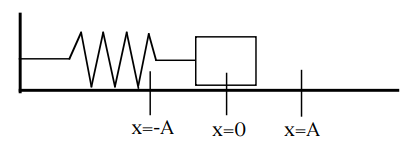
A block on a horizontal frictionless plane is attached to a spring,
as shown above. The block
oscillates along the x-axis with simple
harmonic motion of amplitude A.
21. Which of the following statements about the block is
correct?
(A) At x = 0, its acceleration is at a maximum.
(B) At x = A, its displacement is at a maximum.
(C) At x = A, its velocity is at a maximum.
(D) At x = A, its acceleration is zero.
(B)
A block on a horizontal frictionless plane is attached to a spring,
as shown above. The block
oscillates along the x-axis with simple
harmonic motion of amplitude A.
Which of the following statements about energy is correct?
(A)
The potential energy of the spring is at a minimum at x = 0.
(B)
The potential energy of the spring is at a minimum at x = A.
(C)
The kinetic energy of the block is at a minimum at x =0.
(D) The
kinetic energy of the block is at a maximum at x = A.
(D)
A simple pendulum consists of a l.0 kilogram brass bob on a string
about 1.0 meter long. It has a period of 2.0
seconds. The
pendulum would have a period of 1.0 second if the
(A) string were
replaced by one about 0.25 meter long
(B) string were replaced by
one about 2.0 meters long
(C) bob were replaced by a 0.25 kg
brass sphere
(D) bob were replaced by a 4.0 kg brass sphere
(A)
A pendulum with a period of 1 s on Earth, where the acceleration due
to gravity is g, is taken to another planet,
where its period is
2 s. The acceleration due to gravity on the other planet is most
nearly
(A) g/4 (B) g/2 (C) 2g (D) 4g
(A)
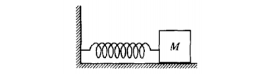
An ideal massless spring is fixed to the wall at one end, as shown
above. A block of mass M attached to the
other end of the spring
oscillates with amplitude A on a frictionless, horizontal surface. The
maximum speed of
the block is vm. The force constant
of the spring is
(A) Mg/A
(B) Mgvm/2A
(C) Mg(vm)2/2A
(D) Mg(vm)2/A2
(D)
Which of the following statements about the block is correct?
A.
At x=0, its velocity is zero.
B. At x=0, its acceleration is at a
maximum.
C. At x=A, its displacement is at a minimum.
D. At
x=A, its velocity is at a maximum.
E. At x=A, its acceleration is maximum
(E)

Which of the following statements about energy is correct?
A.
The potential energy of the spring is at a maximum at x=0.
B. The
potential energy of the spring is at a minimum at x=A.
C. The
kinetic energy of the block is at a maximum at x=0.
D. The
kinetic energy of the block is at a maximum at x=A.
E. The
kinetic energy of the block always equals the potential energy of the spring.
(C)
A simple pendulum consists of a 2.0 kg brass bob on a string about
0.5 m long. It has a period of about 1.42 sec. The pendulum would have
a period of about 5 seconds if the
A. string were replaced by one
25 m long.
B. string were replaced by one 6.2 m long.
C. bob
were replaced by a 0.6 kg brass sphere.
D. bob were replaced by a
7.0 kg brass sphere.
E. bob was released from a 0.5 m height.
(B)
A simple pendulum has a frequency of 0.2 Hz on Earth. It is brought
to Mars where g is 38% of its value on Earth. What will be the
pendulum’s frequency on Mars?
A. 0.12 Hz.
B. 0.2 Hz.
C.
0.08 Hz.
D. 0.52 Hz.
E. 0.32 Hz.
(A)
A simple pendulum of length l, whose bob has mass m, oscillates with a period T. If the bob is replaced by one of mass 4m, the period of oscillation is:
(A) (1/4)T
(B) (1/2)T
(C) T
(D) 2T
(E) 4T
(C)
A particle moves in simple harmonic motion represented by the graph above. Which of the following represents the velocity of the particle as a function of time?
(A) v(t) = 4cos(πt)
(B) v(t) = π cos(πt)
(C) v(t) =
-π2cos(πt)
(D) v(t) = -4 sin(πt)
(E) v(t) = -4π sin(πt)
(E)
The force constant of each spring is most nearly:
(A) 40 N/m
(B) 48 N/m
(C) 60 N/m
(D) 80 N/m
(E)
96 N/m
(A)
When the block is set into oscillation with amplitude A, it passes through its equilibrium point with a speed v. In which of the following cases will the block, when oscillating with amplitude A, also have speed v when it passes through its equilibrium point?
I. The block is hung from only one of the two springs.
II. The block is hung from the same two springs, but the springs are connected in series rather than in parallel.
III. A 0.5 kilogram mass is attached to the block.
(A) None
(B) III only
(C) I and II only
(D) II and
III only
(E) I, II, and III
(A)
The equation of motion of a simple harmonic oscillator is d2x/dt2 = -9x, where x is displacement and t is time. The period of oscillation is
(A) 6π
(B) 9/(2π)
(C) 3/(2π)
(D) 2π/3
(E) (2π/9)
(D)
A frictionless pendulum of length 3m swings with an amplitude of 10 degrees. At its maximum displacement, the potential energy of the pendulum is 10 J. What is the kinetic energy of the pendulum when its potential energy 5 J?
(A) 3.3 J
(B) 5 J
(C) 6.7 J
(D) 10 J
(E) 15 J
(B)
A particle moves in the xy-plane with coordinates given by
x = A cos(wt) and y = A sin(wt)
where A = 1.5m and w = 2.0 rad/s. What is the magnitude of the particle's acceleration?
(A) Zero
(B) 1.3 m/s2
(C) 3.0
m/s2
(D) 4.5 m/s2
(E) 6.0 m/s2
(E)
The length of the pendulum is most nearly:
(A) 1/6 m
(B) 1/4 m
(C) 1/2 m
(D) 1 m
(E) 2 m
(D)
A mass M suspended by a spring with force constant k has a period T when set into oscillation on Earth. Its period on Mars, whose mass is about 1/9 and radius 1/2 that of Earth, is most nearly:
(A) 1/3 T
(B) 2/3 T
(C) T
(D) 3/2 T
(E) 3T
(C)
Which of the following equations could represent the angle θ that the pendulum makes with the vertical as a function of time t?
(A) θ = θmax sin (π/2)t
(B) θ = θmax sin πt
(C) θ = θmax sin 2πt
(D) θ = θmax sin 4πt
(E) θ = θmax sin 8πt
(B)
A 1.0 kg mass is attached to the end of a vertical ideal spring with a force constant of 400 N/m. The mass is set in simple harmonic motion with an amplitude of 10 cm. The speed of the 1.0 kg mass at the equilibrium position is:
(A) 2 m/s
(B) 4 m/s
(C) 20 m/s
(D) 40 m/s
(E)
200 m/s
(A)
A 2 kg mass connected to a spring oscillates on a horizontal, frictionless surface with simple harmonic motion of amplitude 0.4 m. The spring constant is 50 N/m.
The period of this motion is:
(A) 0.04π s
(B) 0.08π s
(C) 0.4π s
(D) 0.8π
s
(E) 1.26π s
(C)
A 2 kg mass connected to a spring oscillates on a horizontal, frictionless surface with simple harmonic motion of amplitude 0.4 m. The spring constant is 50 N/m.
The maximum velocity occurs when the:
(A) potential energy is a maximum
(B) kinetic energy is a minimum
(C) displacement from equilibrium is equal to the amplitude of 0.4 meters
(D) displacement from equilibrium is half the amplitude
(E) displacement from equilibrium is equal to zero
(E)
A girl is swinging on a swing in the sitting position. If she stands up, the the period of the swing will
(1) remain unchanged
(2) increase
(3) decrease
(4) become unpredictable
(3)
The maximum velocity of a particle executing simple harmonic motion with an amplitude 6 cm, is 3.14 ms–1. The period of oscillation is
(1) 120 s
(2) 12 s
(3) 1.2 s
(4) 0.12 s
(4)
One end of a light spiral spring is attached to a hook on the ceiling. A mass m kg hung on the spring stretches it by 10 cm. The mass is pulled down a little and released. The period oscillation of the system in seconds is (take g = 10 ms–2)
(1) 2πm/5
(2) πm/5
(3) π/5
(4) 5π
(3)
You know that the period of oscillation T of a mass m attached to a light spring of force constant k is given by
T =2π√(m/k)
The period of oscillation of such a spring-mass system is found to be 2 s. If the period becomes 3 s when the mass is increased by 2 kg, what is the value of m?
(1) 0.8 kg
(2) 1 kg
(3) 1.2 kg
(4) 1.6 kg
(4)
A particle executing simple harmonic motion along the y-axis has zero displacement at time t = 0. The period of the motion is 1 s. After what time will its kinetic energy be 25% of the total energy?
(1) 1/12 s
(2) 1/6 s
(3) ¼ s
(4) 1 s
(2)
A simple pendulum of period 2 s has a small bob of mass 50 g. The amplitude of oscillation of the bob is 10 cm and it is at a height of 45 cm from the ground in its mean position. While oscillating, the string breaks just when the bob is in its mean position. The horizontal distance R `from the mean position where the bob will strike the ground is nearly
(a) 35.2 cm
(b) 23 cm
(c) 15.3 cm
(d)12.4 cm
(e) 9.4 cm
(e)
A large horizontal surface moves up and down simple harmonically with an amplitude of 1 cm. If a mass of 3 kg (which is placed on the surface) is to remain continually in contact with it, the maximum frequency of the SHM will be
(a) 5 Hz
(b) 2 Hz
(c) 8 Hz
(d) 10Hz
(e) 15 Hz
(a)