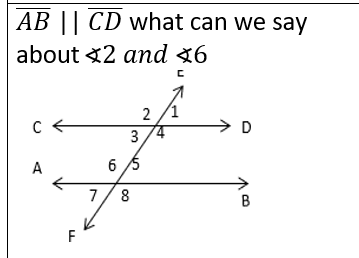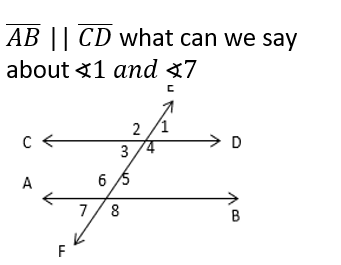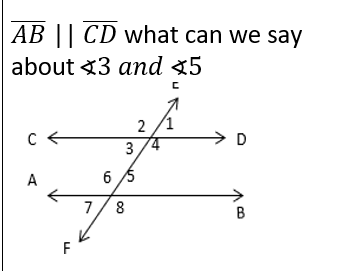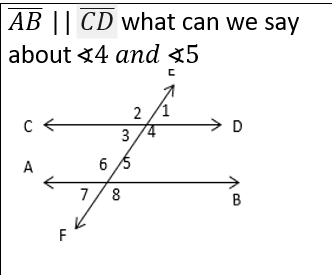SSS (Side-Side-Side)

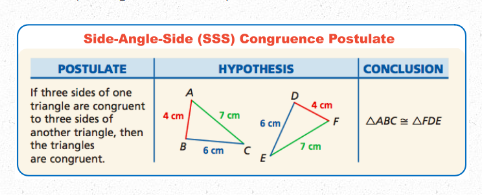
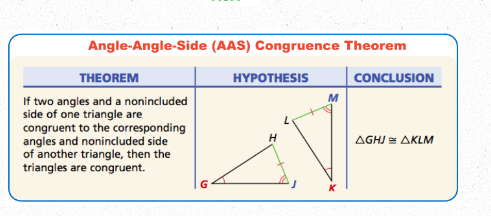
AAS (Angle-Angle-Side)

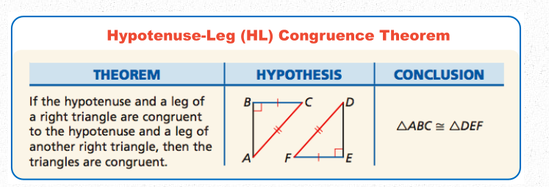
(Rt. Tri. H-L) Right Triangle Hypotenuse Leg

CPCTC

Corresponding Parts of Congruent Triangles are Congruent

*can only use once you have proven triangles congruent*

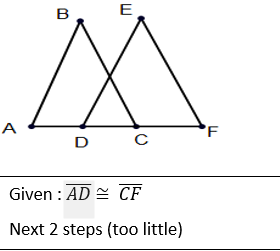
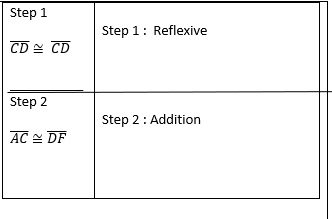
Addition Postulate

If congruent pieces are added to congruent pieces, the whole piece is congruent.

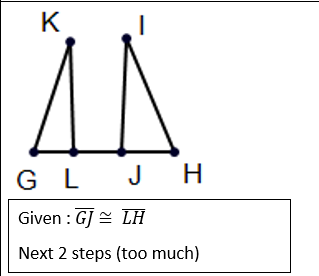
Subtraction Postulate

If a congruent piece is subtracted from a whole congruent piece, the remaining piece is congruent.

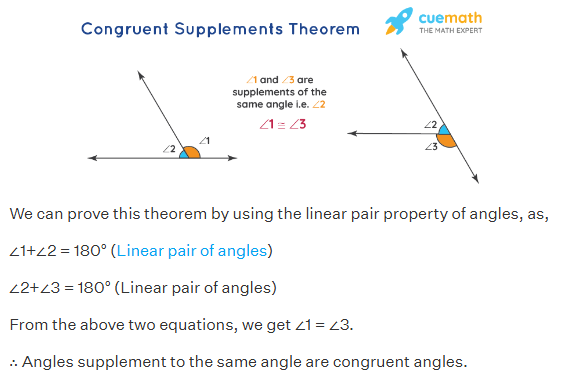
Supplements of Congruent Angles are Congruent

Transitive

A = B

B = C Then we can say...

A = C

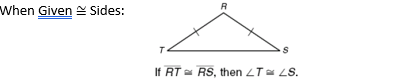
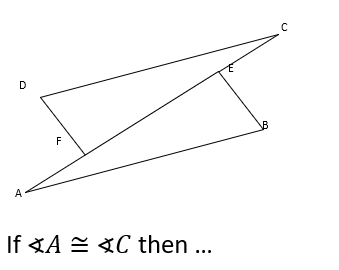
In a triangle if 2 sides are congruent, the opposite angles are congruent.

(you don't have to say its an isosceles triangle first)

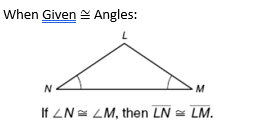
In a triangle if 2 angles are congruent, the opposite sides are congruent.

(you don't have to say its an isosceles triangle first)

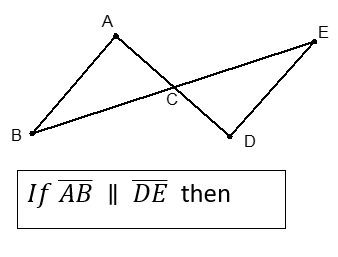
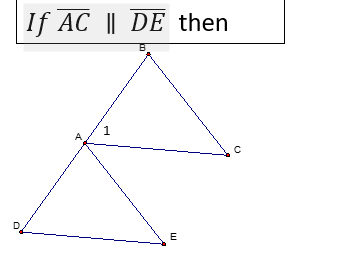
If you need to prove lines Parallel (ll)

if alternate-interior angles are congruent, then lines are parallel

OR

if corresponding angles are congruent, then lines are parallel

OR

if alternate-exterior angles are congruent, then lines are parallel

If using Right Triangle H-L to prove triangles congruent what MUST you include in your proof

You must name the triangles as being Right triangles

Once we proved triangles congruent what can we do?

Prove Corresponding parts congruent by Corresponding Parts of Congruent triangles are congruent (CPCTC)