Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
Geometry Unit 4 - more triangle congruence proofs
front 1 SSS (Side-Side-Side) | back 1 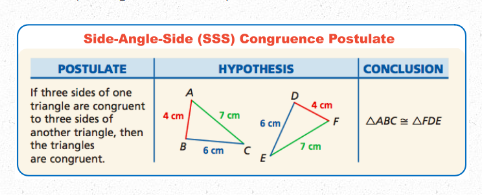 |
front 2 AAS (Angle-Angle-Side) | back 2 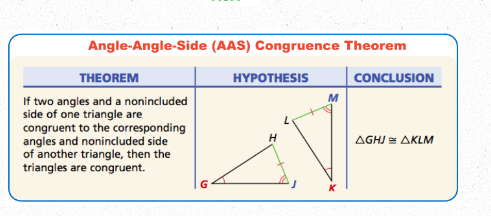 |
front 3 (Rt. Tri. H-L) Right Triangle Hypotenuse Leg | back 3 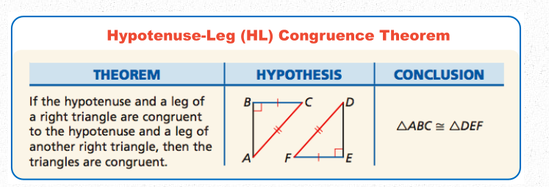 |
front 4 CPCTC | back 4 Corresponding Parts of Congruent Triangles are Congruent *can only use once you have proven triangles congruent* |
front 5 Addition Postulate | back 5 If congruent pieces are added to congruent pieces, the whole piece is congruent. |
front 6 Subtraction Postulate | back 6 If a congruent piece is subtracted from a whole congruent piece, the remaining piece is congruent. |
front 7 Supplements of Congruent Angles are Congruent | back 7 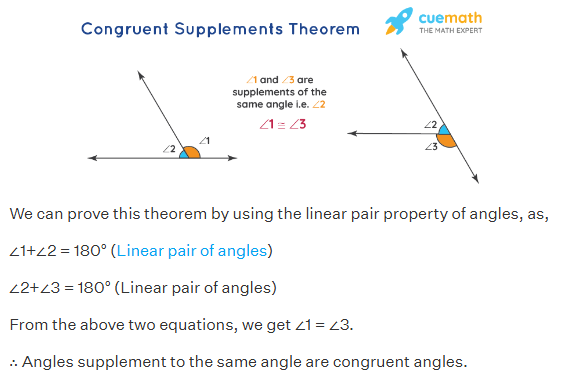 |
front 8 Transitive | back 8  A = B B = C Then we can say... A = C |
front 9 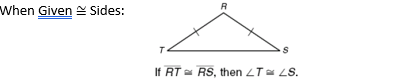 | back 9 In a triangle if 2 sides are congruent, the opposite angles are congruent. (you don't have to say its an isosceles triangle first) |
front 10 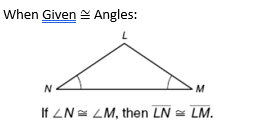 | back 10 In a triangle if 2 angles are congruent, the opposite sides are congruent. (you don't have to say its an isosceles triangle first) |
front 11 If you need to prove lines Parallel (ll) | back 11 if alternate-interior angles are congruent, then lines are parallel OR if corresponding angles are congruent, then lines are parallel OR if alternate-exterior angles are congruent, then lines are parallel |
front 12 If using Right Triangle H-L to prove triangles congruent what MUST you include in your proof | back 12 You must name the triangles as being Right triangles |
front 13 Once we proved triangles congruent what can we do? | back 13 Prove Corresponding parts congruent by Corresponding Parts of Congruent triangles are congruent (CPCTC) |
front 14 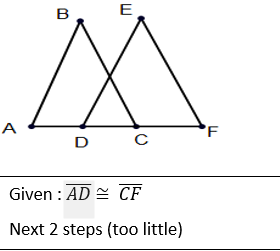 | back 14 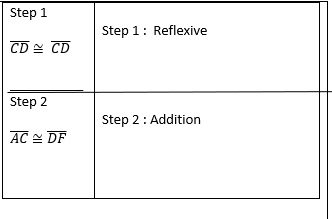 |
front 15 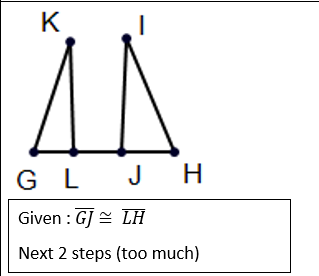 | back 15  |
front 16 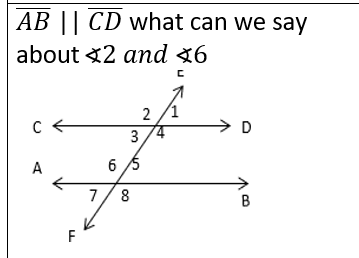 | back 16  |
front 17 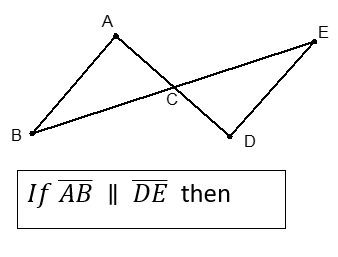 | back 17  |
front 18 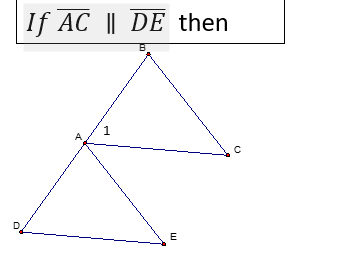 | back 18  |
front 19 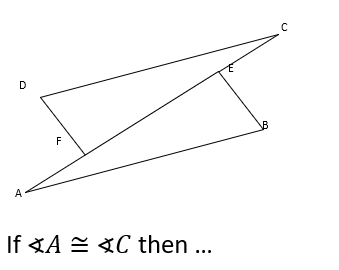 | back 19  |
front 20 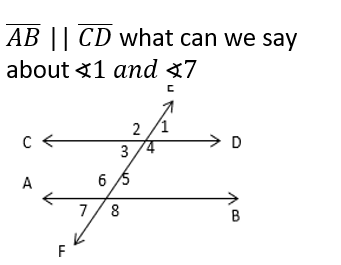 | back 20  |
front 21 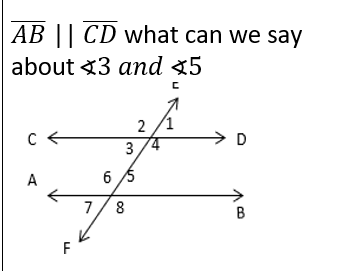 | back 21  |
front 22 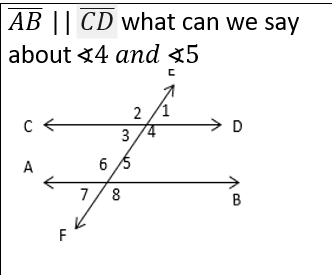 | back 22  |