Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
FINAL EXAM
front 1 Anything that demands mental or physical effort | back 1 Work |
front 2 Mechanical work is equal to the product of _______ and
________? | back 2 the magnitude of a force applied against an object and the distance the object moves in the direction of the force moving the applied force |
front 3 Work can only be done with __________? | back 3 movement |
front 4 Because work is the product of ______ and ______, the units for work are units of _____ by ______? Name all units for work, force and length? What does one joule equal? | back 4 force and displacement force x units of length ft-lb |
front 5 U = F(d) describes the work done by a ________? | back 5 constant force. force whose magnitude varies |
front 6 To determine the amount of work done on an object, we need to know
three things: | back 6 force direction displacement |
front 7 A discus thrower exerts an average force of 1000 N against the discus while the discus moves through a displacement of 0.6 m in the direction of this force. How much work did the discus thrower do to the discus? | back 7 U = F(d) U = (1000 N)(0.6 m) |
front 8 A weightlifter bench presses a 1000 N barbell. He begins with his arms extended and the barbell 75 cm above his chest. The lifter then lowers the barbell and stops it when it is 5 cm above his chest. He pauses there and then lifts the barbell upward away from his chest and back to the original starting position 75 cm above his chest. The average force exerted on the barbell by the lifter while lowering the weight is 1000 N upward. The average force exerted by the lifter while raising the weight is also 1000 N upward. So the average force exerted on the barbell by the lifter is 1000 N for the whole lift. How much work did the lifter do on the barbell from the start until the finish of the lift? | back 8 High to low so 75-5…..= -70 cm displacement |
front 9 done by a force acting on an object if the object is displaced in the same direction as the force. Describe an examle with a pitcher, weightlifter and a high jumper? | back 9 Positive Work A pitcher does positive work against a baseball when
throwing it |
front 10 done by a force acting on an object when the object is displaced in the direction opposite the force acting on it. Give examples with a first basemen, weightlifter, and a gymnast? | back 10 Negative Work A first baseman does negative work against the ball when
catching it |
front 11  Is it positive or Negative work when doing a pull-up? What tends to be negative work? | back 11 Positive work…most concentric muscle action |
front 12 When a muscle contracts and the force results in the points of
attachment moving in the direction of the muscle force | back 12 Positive muscle work Concentric |
front 13 When a muscle contracts and the points of attachment move away from
the direction of the muscle force | back 13 Negative muscle work Eccentric |
front 14 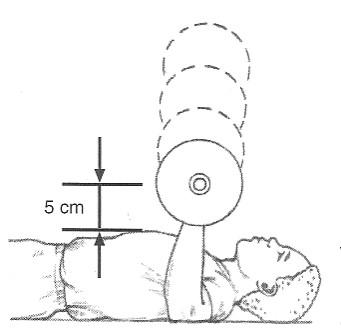 Calculate work done while lowering the bar? | back 14 U = 1000N(-0.7m) |
front 15 How much work is being done? (raise bench press up to 75 m then bring it down to 5 cm and then back up) explain? | back 15 -700 + 700 = 0 Pos and neg work will cancel each other out |
front 16 the rate of doing work, or how much work is done in a specific amount of time. | back 16 Power |
front 17 two equations for power? ∆t = ? Units of power are units of ____ divided by units of _____. | back 17 Power = Work/time time taken to do the work work time |
front 18 Joules (J) divided by seconds are called ? | back 18 watts (W) |
front 19 1 W = ? | back 19 1 J/s |
front 20 In this equation: P = F(d)/ ∆t...what can you also write it as
dealing with velocity and why? When looking at angular movements power
can be expressed as: | back 20 Because velocity is the displacement / time some also identify power
as: Torque x angular velocity |
front 21 Human movement involves _____ displacement being performed by joints | back 21 angular |
front 22 Displacement can be _____ or ______? | back 22 linear or angular |
front 23 Peak Power is also referred to as ? | back 23 Instantaneous Power |
front 24 The highest power value achieved during the movement being observed | back 24 Peak Power / Instantaneous Power |
front 25 The product of the average force and the average velocity of an entire movement | back 25 Average Power |
front 26 The product of the joint torque and angular velocity | back 26 Internal (Joint) Power |
front 27 When we examine joint movements, what 2 things do you look at and
why? The balance between these may change as we go through a _______
during a particular movement | back 27 torque or angular velocity may dominate in producing the highest power values joint ROM From a training perspective it is important to understand which factor is most important during certain movements in order to optimize training (whether in the weight room or during sport specific practice drills)...Look at if its torque or velocity that is the weak link and then work on improving that to inc power |
front 28 The aggregate of multiple joint powers resulting in a body movement? What is a common method for analyzing whole body power? How would you analyze that movement? | back 28 External (Whole-body) Power The vertical jump Isolate joints and identify as upper or lower body power….ex. With vertical jump as a lower body power the subject must not use their arms and have their arms on their hips |
front 29 What are 3 schools of thought when trying to train to maximize power output? | back 29 1. Lower Intensity Loads |
front 30 As wee get older what do we develop? What is that defined as? What does this effect? | back 30 As we get older… develop sarcopenia…dec in cross sectional area…less ability to recruit type 2 muscle fibers |
front 31 Ballistic exercises focus more on ? | back 31 velocity |
front 32 Heavy resistance exercises focus more on ? | back 32 strength |
front 33 Describe force-velocity curve? | back 33 As velocity inc force goes down and as velocity dec, force inc |
front 34 When attempting to increase power output there are 3 key
elements: | back 34 strength force development high forces velocity optimum load |
front 35 Maximization of overall strength levels results in significant improvements in _____? Thus training should establish adequate ____? | back 35 muscular power strength |
front 36 Sufficient _____ is needed prior to incorporating activities targeting _____ development | back 36 strength power |
front 37 (RFD) | back 37 Rate of Force Development |
front 38 Rate of Force Development is determined from ? RFD = ? The steeper the slope means what? | back 38 the slope of the force time curve ∆force/ ∆time The better the rate of force development |
front 39 As a muscle’s velocity of contraction increases, its __________ decreases | back 39 maximum force of contraction |
front 40 The maximum power output occurs when? | back 40 at a velocity approximately one-half the muscle’s maximum contraction velocity. |
front 41 Mechanically defined as the capacity to do work | back 41 Energy |
front 42 Mechanical energy comes in what two forms? | back 42 Kinetic Energy |
front 43 Energy due to motion | back 43 Kinetic Energy |
front 44 Energy due to position | back 44 Potential Energy |
front 45 A moving object has the capacity to do work due to its motion | back 45 kinetic energy |
front 46 The kinetic energy of an abject is affected by the _____ and _____ of the object | back 46 mass and velocity |
front 47 An object that is stationary has no ? | back 47 kinetic energy |
front 48 KE formula= | back 48 1/2 m x v squared m = mass |
front 49 To determine the kinetic energy of an object, the _____ and _____ must be known | back 49 mass and velocity |
front 50 How much kinetic energy does a baseball thrown at 80 mph (35.8 m/s) have? The mass of the baseball is 145 g (0.145 kg). | back 50 KE = 1/2 mv 2 |
front 51 mass x velocity squared is equal to which unit? Which is also equivalent to? | back 51 Units of Kinetic energy are mass times velocity squared |
front 52 The energy (capacity to do work) an object has due to its position | back 52 Potential Energy |
front 53 What are the two types of potential energy? | back 53 Gravitational Potential Energy Strain Energy |
front 54 Energy due to an object’s position relative to the Earth | back 54 Gravitational Potential Energy |
front 55 Energy due to the deformation of an object | back 55 Strain Energy |
front 56 Related to the object’s weight and its elevation or height above the ground or some reference | back 56 Gravitational Potential Energy |
front 57 PE = ? Explain what each thing stands for? | back 57 Wh or mgh W = weight |
front 58 Greater the mass and the higher up it is…the greater the ? | back 58 gravitational potential energy |
front 59 How much gravitational potential energy does a 700 N ski jumper have when taking off from a 90 m jump? | back 59 PE = Weight x height |
front 60 Related to the objects stiffness, material properties, and its deformation | back 60 Strain Energy |
front 61 The greater the _______ of an object, the greater the strain energy | back 61 deformation |
front 62 1/2 k∆x2 what does k and delta x stand for? | back 62 Strain Energy k = stiffness or spring constant of material |
front 63 Name 2 Strain Energy Examples? | back 63 Lacrosse Shaft |
front 64 Name 2 Strain Energy Examples in the body? | back 64 Muscle Tendons |
front 65 Describes motion | back 65 Kinematics |
front 66 Kinematics can be ______ or ______ | back 66 Can be Qualitative or Quantitative |
front 67 Kinematic description of kicking a soccer ball? | back 67 Qualitatively…good, bad, okay? |
front 68 A2 + B2 = C2 | back 68 Pythagorean Theorem |
front 69 Trigonometric Functions how to get just theta? cosθ =? how to get just theta? tanθ =? | back 69 opposite/hypotenuse θ = arcsin{opposite/hypotenuse} adjacent/hypotenuse θ = arccos{adjacent/hypotenuse} opposite/adjacent |
front 70 The branch of dynamics concerned with the description of motion | back 70 Linear Kinematics |
front 71 The outcomes of many sporting events are kinematic measures..such as? | back 71 Speed |
front 72 The action or process of a change in position | back 72 Motion |
front 73 Moving involves a change in position from ______ to _____? | back 73 one point to another. |
front 74 What two things are necessary for motion to occur | back 74 Space: to move in |
front 75 3 motion Movement Classifications? | back 75 Linear |
front 76 Referred to as translation | back 76 Linear Motion |
front 77 Occurs when all points on a body or object move the same distance, in the same direction, and at the same time | back 77 Linear Motion |
front 78 Linear Motion can happen in what two ways? | back 78 Rectilinear Translation |
front 79 Occurs when all points on a body or object move in a straight line so the direction of motion does not change, the orientation of the object does not change, and all points on the object move the same distance | back 79 Rectilinear Translation/Motion |
front 80 Occurs when all points on a body or object move so that the orientation of the object does not change and all points on the object move the same distance | back 80 Curvilinear Translation/Motion |
front 81 Paths followed are curved, so the direction of motion is constantly changing | back 81 Curvilinear Translation/Motion |
front 82 Sledding and skiing are which motions? | back 82 Sledding is in a straight line |
front 83 Referred to as Rotary Motion or Rotation | back 83 Angular Motion |
front 84 Occurs when all points on a body or object move in circles (or parts of circles) about the same fixed central line or axis | back 84 Angular Motion |
front 85 Angular motion can occur about an axis within _____ or outside ______? | back 85 the body of the body |
front 86 Combination of both Angular and Linear Motions | back 86 General Motion |
front 87 Most common type of motion exhibited in sports and human movement. | back 87 General Motion |
front 88 Combining the Angular Motion of the limbs can produce __________ of one or more body parts | back 88 Linear Motions |
front 89 Location in space | back 89 Position |
front 90 Strategies employed in sports often depend on where players on each team are _________? | back 90 positioned |
front 91 20 yd from the goal and 15 yd from the left sideline...what is his full position? What would it be on a Cartesian Coordinate System? | back 91 His full position would be 20 yd from the goal line and 15 yd from the left sideline. Identify the running back’s position with the two numbers corresponding to his x- and y-coordinates in yards as (15, 80) -he traveled 80 yards |
front 92 In 3 Dimensions, we would need ____ numbers to describe the position of an object in space? How would you do this? | back 92 three x-axis |
front 93 If the ball were: | back 93 (3, 2, 4) |
front 94 Most commonly used unit of distance and displacement is the | back 94 meter (m) |
front 95 1 km = _____ m | back 95 1000 1/100 1/1000 |
front 96 Scalar Quantity | back 96 Distance |
front 97 Vector Quantity | back 97 Displacement |
front 98 For displacement, Direction | back 98 (+)(-) i.e. NE, SW i.e. Left, Right, Up, Down |
front 99 Describe coordinates for northeast, NW, SW, and SE? | back 99 NE= (+,+) NW= (-, +) SW= (-,-) SE= (+,-) |
front 100 Simply a measure of the length of the path followed by the object whose motion is being described...example? | back 100 Distance Travelled When a runner goes partially around a track |
front 101 Distance Travelled...from its what to what? | back 101 From its starting (initial) position |
front 102 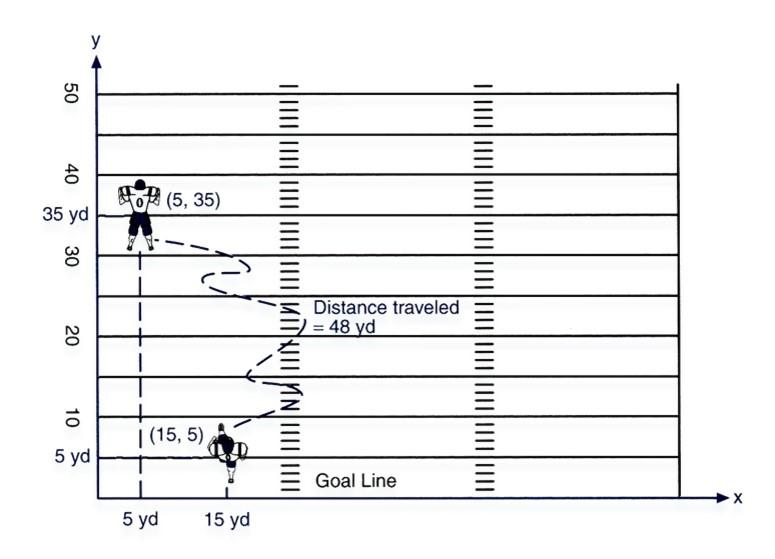 distance and displacement? | back 102 The length of the path of his run is 48 yd. |
front 103 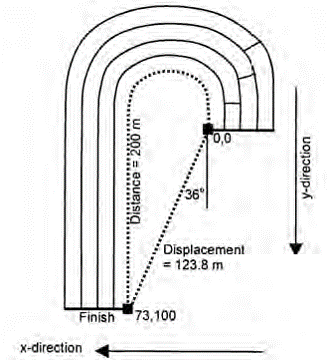 The straight-line distance in a specific direction from initial (starting) position to final (ending) position... example of this? | back 103 Displacement When a runner goes partially around a track |
front 104 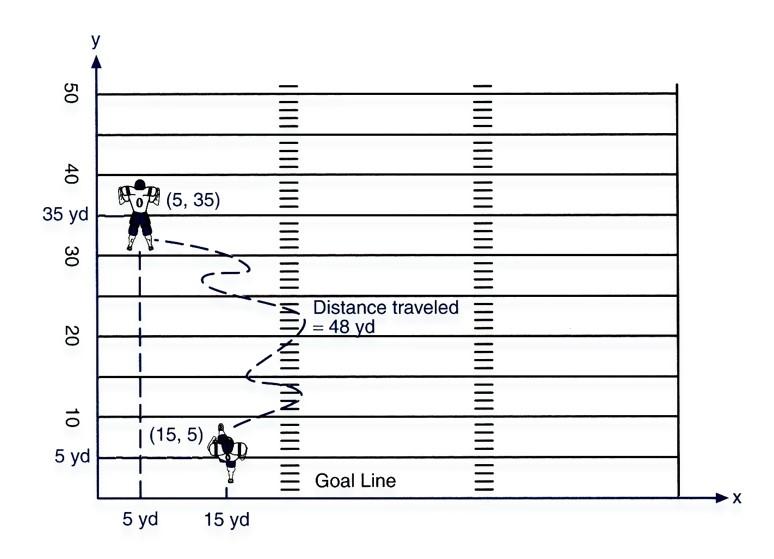 A football player receives a kickoff at his 5 yd line, 15 yd from the
left sideline. | back 104 dy = ∆y = yf - yi = 35 yd - 5 yd = +30 yd dx = ∆x = xf - xi = 5 yd - 15 yd = -10 yd |
front 105 The distance measured in a straight line from the initial position to the final position | back 105 Resultant Displacement |
front 106 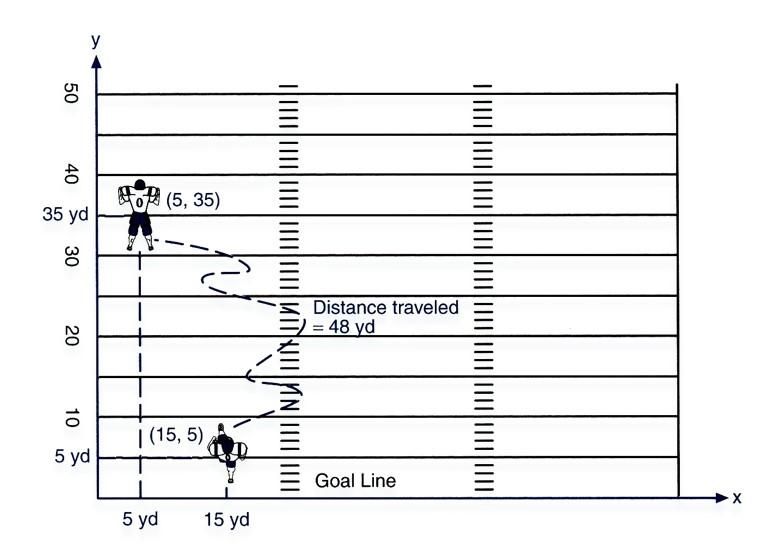 Resultant Displacement here? | back 106 A2 + B2 = C2 |
front 107 The rate of motion | back 107 Speed |
front 108 Speed is a _______ quantity? | back 108 Scalar Quantity |
front 109 Calculated as distance/∆t | back 109 Speed |
front 110 The rate of motion in a specific direction | back 110 Velocity |
front 111 Velocity is a _________ quantity? | back 111 Vector Quantity |
front 112 Speed involves what and velocity involves what? | back 112 Magnitude Magnitude |
front 113 Calculated as displacement/∆t | back 113 Velocity |
front 114 position2 – position1 divided by | back 114 Velocity |
front 115 The distance travelled divided by the time it took to travel that distance...its formula? | back 115 Average Speed s =ℓ/∆t |
front 116 When comparing 2 peoples average speed what can you analyze? | back 116 Here we can determine where they are stuggling and from here postentially train their weak areas. Is it physiological or mechnical. |
front 117 Comparison of two 100 m dash performances Ben Johnson 9.79 s Carl Lewis 9.92 s Comparison of the performances for the first 50 m of the 100 m race Ben Johnson 5.50 s Carl Lewis 5.65 s | back 117 s = 100 m/9.79 s = 10.21 m/s s = 100 m/9.92 s = 10.08 m/s s 0-50 m = 50 m/5.50 s = 9.09 m/s s 0 - 50 m = 50 m/5.65 s = 8.85 m/s |
front 118 Because description of velocity must include an indication of both
the _____ and the _____ of motion | back 118 direction magnitude positive negative both |
front 119 The displacement of an object divided by the time it took for that displacement...formula for it? | back 119 Average Velocity v = d/∆t |
front 120 Mechanically defined as the rate of change in velocity, or the change in velocity occurring over a given time interval...formula for it and explain each part? | back 120 Acceleration a = ∆v/∆t or a = average acceleration |
front 121 In general usage, the term accelerating means what? | back 121 speeding up, or increasing in velocity. |
front 122 If vf is greater than vi, acceleration is a _____ number indicating what? | back 122 positive the body in motion may have sped up during the time period in question |
front 123 If vf is less than vi, acceleration is a ______ number indicating what? | back 123 negative the resulting average acceleration is negative…you slowed down |
front 124 Because it is sometimes appropriate to label the direction of motion as positive or negative, a positive value of acceleration may not mean what? If the direction of motion is described in terms other than positive or negative, a positive value of acceleration _____ indicate that the body being analyzed has speeded up | back 124 that the body is speeding up does |
front 125 If a sprinter’s velocity is 3 m/s on leaving the blocks and is 5 m/s one second later, calculation of the acceleration is? | back 125 a = v2 – v1/∆t |
front 126 As long as the direction of motion is described in terms other than positive or negative, negative acceleration indicates ? | back 126 that the body in motion is slowing down, or that its velocity is decreasing |
front 127 When a base runner slides to a stop over home plate, acceleration is negative. If a base runner’s velocity is 4 m/s when going into a 0.5 s slide that stops the motion? calculate acceleration | back 127 v1 = 4 m/s, v2 = 0, t = 0.5 s a = v2 – v1/∆t |
front 128 The third alternative is for acceleration to be equal to ? | back 128 0 |
front 129 Acceleration is 0 whenever ? When could we see this? | back 129 velocity is constant, that is, when vi and vf are the same. In the middle of a 100 m sprint, a sprinter’s acceleration should be close to 0, because at that point the runner should be running at a constant, near maximum velocity |
front 130 During a 100 m race, describe acceleration during the start, middle and end? | back 130 pos at start constant velocity in middle giving 0 acceleration neg at end |
front 131 When speeding up, acceleration is in the direction _______? | back 131 of the motion |
front 132 When slowing down, acceleration is in the _____ direction of the motion | back 132 opposite |
front 133 Speeding up (+) in the positive (+) direction results in a
? | back 133 positive (+) sign negative (-) sign negative (-) sign positive (+) sign |
front 134 Angular Kinematics is similar to _____? How is it different? This involves different what? Give a few examples? | back 134 Linear Kinematics Dealing with Rotary Motions (rather than linear) Different equations to account for rotary motion |
front 135 is measured as the sum of all angular changes undergone by a rotating body | back 135 Angular Distance |
front 136 Angle of elbow joint changes from 90º to 160º | back 136 70º |
front 137 is assessed as the difference in the initial and final positions of the moving body | back 137 Angular Displacement |
front 138 If the angle of elbow joint changes from 90º to 160º then back to 90º the displacement would be? | back 138 0º |
front 139 Like linear displacement, angular displacement is defined both by ____ and ______? Clockwise is ? | back 139 magnitude and direction negative positive |
front 140 Angular Distance & Displacement can be recorded in what three different units of measure? Which is most common? Which is preferred for calculations? | back 140 1. Degrees – most common |
front 141 SI units for position, displacement or velocity, and acceleration? | back 141 position- radians dis and vel- rad x s-1 acc- rad x s-2 |
front 142 Size of the angle subtended at the center of a circle by an arc equal in length to ? One radian is equivalent to ? One complete circle is ? The radius of a circle fits around its circumference ____ times ? ____ radians in a half circle | back 142 the radius of the circle 57.3° 2π radians 2π 1π |
front 143 We also know that the entire circle encompasses a total of ____ degrees? | back 143 360° |
front 144 How do you convert from degrees to radians? Example: convert 276 degrees to radians | back 144 simply divide 276 by 57.3 = 4.82 radians |
front 145 How do you convert from radians to degrees? Example: convert 2.3 radians to degrees | back 145 simply multiply 2.3 by 57.3 = 132 degrees |
front 146 defined as one complete turn | back 146 Revolution |
front 147 How do you convert degrees into revolutions? | back 147 Degrees / 360 = revolution |
front 148 σ | back 148 Angular Speed |
front 149 Defined as: the angular distance covered divided by the time interval or which the motion occurred what kind of quantity? | back 149 Angular Speed Scalar quantity |
front 150 ϕ | back 150 angular distance |
front 151 angular distance/change in time | back 151 Angular Speed formula |
front 152 Change in angular displacement that occurs during a given period of time? what kind of quantity? | back 152 Angular Velocity vector |
front 153 angular displacement/ change in time | back 153 Angular Velocity formula |
front 154 ω | back 154 Angular Velocity |
front 155 Ɵ | back 155 angular displacement |
front 156 ω = Ɵ2 – Ɵ1 /t 2 – t1 | back 156 Angular Velocity formula |
front 157 Angular Speed & Velocity are recorded in: Revolutions per second or per minute = ? | back 157 deg/s rad/s rev/s or rpm |
front 158 The rate of change in angular velocity? what type of quantity? | back 158 Angular Acceleration vector |
front 159 α | back 159 Angular Acceleration |
front 160 ω2 – ω1 /t 2 – t1 | back 160 Angular Acceleration |
front 161 A golf club is swung with an average angular acceleration of 1.5
rad/s2. | back 161 Known: Formula: |
front 162 Just as with linear acceleration, angular acceleration may be what? | back 162 positive, negative, or zero |
front 163 Positive angular acceleration: | back 163 positive negative |
front 164 Negative angular acceleration: | back 164 negative positive |
front 165 The greater the radius is between a point on a rotating body and the axis of rotation, the greater the __________ undergone by that point during an angular motion | back 165 linear distance |
front 166 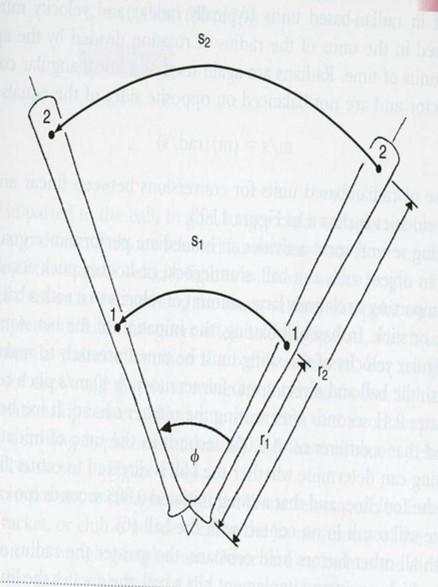 Describe this pic? Formula to use here that relates angular and linear relationships? | back 166 Point 2 traveling further than point 1…means it is moving faster (linear velocity) The angular velocity is the same though S = rϕ |
front 167 = r ω explain each part For this formula to work, what must happen? | back 167 Linear Velocity Where: angular velocity must be in rad/s |
front 168 Two baseballs are consecutively hit by a bat. The first ball is hit
20 cm from the bat’s axis of rotation and the second ball is hit 40 cm
from the bat’s axis of rotation | back 168 Known: Formula: |
front 169 Can you think of examples of sport/exercise where we manipulate all of these variables? (with a lever and two points on it-related to baseball and golf) | back 169 Baseball pitchers are usually tall with long arms |
front 170 Longer limbs are more advantageous for imparting _____ linear velocities | back 170 greater |
front 171 In Athletic Coaching, | back 171 limb length |
front 172 In Training principles, | back 172 angular velocity force generating capacity velocities |
front 173 Using these principles of smaller distance between point and axis of rotation to reduce an opponents performance in baseball and tennis? | back 173 Baseball Pitcher Cant extend arm fully to get a good lever arm length to maximize linear velocity |
front 174 What are Newton’s 3 Laws of Motion? | back 174 First Law: Law of Inertia |
front 175 Law of Inertia | back 175 1st law |
front 176 Law of Acceleration | back 176 2nd law |
front 177 Law of Action/Reaction | back 177 3rd law |
front 178 A body will maintain a state of rest or constant velocity unless acted upon by an external force that changes the state | back 178 1st Law – Law of Inertia |
front 179 A motionless object will remain _________ unless there is a net force (a force not counteracted by another force) acting on it | back 179 motionless |
front 180 A body travelling with a constant speed along a straight path will
continue its motion unless ? | back 180 acted on by a net force that alters either the speed or the direction
of the motion. |
front 181 The property of an object that causes it to remain in a state of either rest or motion | back 181 Inertia |
front 182 Because of Inertia, ______ is needed to change the velocity of an object | back 182 force |
front 183 The amount of force needed to alter the object’s velocity is directly related to ? | back 183 the amount of inertia it has |
front 184 The measure of (linear) inertia in a body is its ? Give an example or a comparison? | back 184 mass (the quantity of matter it posses) |
front 185 inertia is most in what football players? | back 185 offensive and defensive lines in football have more inertia...they are big |
front 186 A force applied to a body causes an acceleration of that body of a magnitude proportional to the force, in the direction of the force, and inversely proportional to the body’s mass. | back 186 2nd Law – Law of Acceleration |
front 187 When a ball is thrown, kicked, or struck with an implement, it tends to travel in what direction? | back 187 the direction of the line of application of the applied force. |
front 188 The greater the amount of force applied, the greater the _____ of the ball. | back 188 speed |
front 189 describes the relationship between an object's mass and the amount of force needed to accelerate it. | back 189 Newton's second law of motion |
front 190 Formula for force? | back 190 Force = mass x acceleration |
front 191 Force = mass x acceleration: | back 191 force |
front 192 The Law of Acceleration dictates that when sufficient _______ is applied to a mass, an acceleration will occur (F = ma) Because acceleration is the rate of change in velocity, this equation can be written as? How do we turn that formula into impulse? | back 192 force F = m(v-u)/t v=final vel and u= initial vel Ft = m(v-u) |
front 193 The product of Force (F) and the time over which the force is applied is called? | back 193 Impulse |
front 194 We manipulate impulse all the time to maximize sport/exercise performance to do what? The greater the time we apply the force the greater the ? Examples with bobsledding, baseball, shot-put and triple extension? | back 194 enhance the acceleration and subsequent velocity of an object acceleration Bobsled…running and pushing to apply force over a given amount of time to inc acceleration Baseball..windup in pitch Shot-put, etc. (spin around 1st before throwing) Triple Extension – |
front 195 during Gait with impulse, the objective is to apply ______ for the longest possible time? | back 195 the largest force |
front 196 The greater the impulse the greater the change in ? How do we
optimize this during gait? | back 196 momentum breaking impulse (ex. Heel strike) propulsive impulse |
front 197 Describe impulse graph for gait? | back 197 area under curve is the braking impulse and is negative propulsive impulse is on positive part of graph |
front 198 Elite sprinters land with their foot about 6cm where? | back 198 in front of the body twice |
front 199 How do you improve propulsive impulse? How does this improve it? “Short contact times of elite sprinters are the result of their __________, rather than the being the cause of them” Blazevich 2007. When in the air are we accelerating? how does this relate? | back 199 Improve hip extension (force & ROM) to lengthen the propulsive impulse This increases the force and the time over which the force is applied by keeping feet on ground longer fast running speed When in air we aren’t accelerating |
front 200 Impulse is related to ? The greater the impulse (Ft) the greater the ? Give an example with a car? | back 200 momentum change in momentum Example - pushing a car |
front 201 Ft = mv – mu | back 201 impulse equation |
front 202 The product of mass and velocity is ? Describe this? | back 202 momentum The faster an object moves, the more momentum it has |
front 203 Linear Momentum equation | back 203 L = mv L = linear momentum |
front 204 Newton’s 1st Law states that the velocity of an object is constant if the net force acting on the object is ? | back 204 zero |
front 205 If the velocity of an object is constant, then its momentum is constant as well, why? | back 205 since mass doesn’t change and vel is constant |
front 206 L = constant if ∑F = ? | back 206 0 |
front 207 Since velocity is a vector quantity, momentum is also a vector quantity and contains both ______ and _______? | back 207 magnitude and direction |
front 208 Units of momentum are units of ____ multiplied by units of _____ and are expressed in terms of ? | back 208 mass velocity kg ● m/s |
front 209 The total momentum of a system of objects is _____ if the net external force acting on the system is zero | back 209 constant |
front 210 ∑(mu) initial = m1u1 + m2u2 + m3u3 = m1v1 + m2v2 +m3v3 = ∑(mv) final Describe each symbol? | back 210 if Li and Lf are constant Li = initial linear momentum |
front 211 For every action, there is ? What law? | back 211 an equal and opposite reaction. 3rd law |
front 212 When one body exerts a force on a second, the second body exerts a reaction force that is _____ in magnitude and ______ in direction on the first body | back 212 equal opposite |
front 213 When a person leans with a hand against a rigid wall, the wall does what? The harder the hand pushes against the wall, the greater is the what? | back 213 pushes back on the hand with a force that is equal and opposite to that exerted by the hand on the wall. amount of pressure felt across the surface of the hand where it contacts the wall. |
front 214 Where are collisions are common in sport? | back 214 Baseballs collide with bats, soccer balls collide with feet, defensive linemen collide with offensive linemen |
front 215 When two objects collide in a head-on collision, their combined ______ is conserved? What can this help us know? | back 215 momentum This principle can be used to predict the post-collision movements of the objects in certain situations if we know their masses and their pre-collision velocities |
front 216 Yellow car bumps into parked green car? Find the green cars momentum? my = 1,814 kg mg = 2,268 kg my = 1,814 kg mg = 2,268 kg | back 216 (my)(uy) + (mg)(ug) = (my)(vy) + (mg)(vg) (1,814 kg)(8.94 m/s) + (2,268 kg)(0 m/s) = (1,814 kg)(0 m/s) + (2,268 kg)(vg) 16,217.16 kg-m/s = (2,268 kg)(vg) 7.15 m/s = vg |
front 217 In a perfectly inelastic collision, momentum is still conserved, but rather than bouncing off each other, the objects in the collision do what? Formula for this? | back 217 stay together after the collision and move with the same velocity (m1)(u1) + (m2)(u2) = (m1 + m2)(v) |
front 218 Actual collisions are also affected by other factors such as the extent to which the players become ______, by whether one or both players remain on their _____, and by the _____ of the collision. | back 218 entangled feet elasticity |
front 219 In the absence of external forces, the total momentum of a given system remains ? | back 219 constant |
front 220 A 90 kg hockey player traveling with a velocity of 6 m/s collides head-on with an 80 kg hockey player traveling at 7 m/s. If the two players entangle and continue traveling together as a unit following the collision, what is their combined velocity? | back 220 m1 = 90 kg m1v1 + m2v2 = (m1 + m2)(v) |
front 221 Remember, total momentum of a system must remain the same, because momentum is conserved unless ? | back 221 ….an external force acts. |
front 222 How can you ensure in sports that you don't get pushed backwards? 1. We can manipulate your _____ so your momentum is greater than
your opponents (depending on the comparison of your ______, your
velocity may need to be very great or only slightly more) | back 222 velocity masses a force to the ground applies an equal and opposite force back at you not in line zero Tackle them from the side. |
front 223 2 Classification of Forces? | back 223 Internal |
front 224 Those forces that act on an object as a result of its interaction with the environment surrounding it | back 224 External Forces: |
front 225 The property of an object to resist changes in its linear motion....dependent only to the ______ of the object (no fixed point – object moves as a unit) | back 225 Linear inertia mass |
front 226 The larger the mass the more _____ | back 226 inertia |
front 227 “We use _________ because we are describing the propensity form masses which are at a distance from the center of rotation, to resist changes to ________” | back 227 Moment of Inertia aka Angular inertia ( their state of motion |
front 228 The property of an object to resist changes in its angular motion Dependent on the ____ and the ______ of the mass | back 228 Angular inertia (aka – moment of inertia) mass distribution |
front 229 The total moment of inertia is the sum of the masses of all these particles multiplied by the distance of each of those particles from the center of rotation | back 229 Angular inertia (aka – moment of inertia) |
front 230 The more particles that are _____________, the larger is the moment of inertia. | back 230 further from the pivot |
front 231 Doubling the mass – ______ the inertia | back 231 doubles quadruple |
front 232 Describe how radius plays a big role in angular inertia? | back 232 Radius or how far it is fro center of rotation will determine and effect angular inertia…gets harder to rotate something further away from axis |
front 233 If an object is unconstrained and free to rotate about any axis, it will rotate through its center of gravity | back 233 Angular inertia about center of gravity |
front 234 If an object rotates about a fixed axis that does not pass through the Center of Gravity | back 234 Angular inertia about Eccentric Axes |
front 235 Represents the object’s mass distribution with respect to a given axis of rotation (a distance) | back 235 Radius of gyration |
front 236 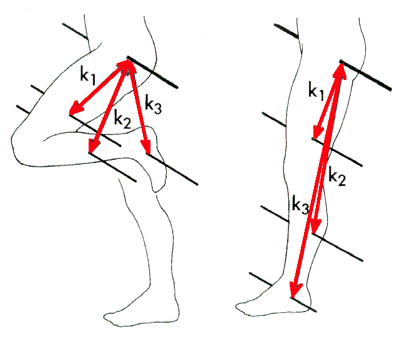 explain this picture? | back 236 Reduces moment of inertia when we bring the lower leg up…results in less force needed to bring leg forward Knee angle affects the moment of inertia of the swing leg with respect to the hip because of changes in the radius of gyration for the lower leg |
front 237 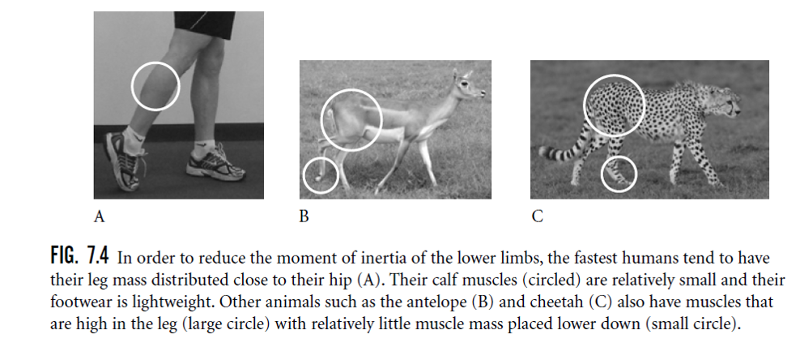 explain this picture? | back 237 Reduces MOI with skinny ankles or skinny legs…makes it easier to move those limbs |
front 238 How do we manipulate our bodies in sport and exercise to optimize inertia? What about sporting implements? | back 238 Keep the load closer to you |
front 239 When a figure skater is spinning, what happens as she brings her arms in close to her trunk? As she abducts her arms? | back 239 Faster they spin if they keep all their mass as close as they can to their center of rotaion |
front 240 What about a tight rope walker? | back 240 Wont rotate as easily with a big pole (holding it as they walk across) because their radius is huge. Also keep arms out when walking on a balance beam to increase inertia and therefore they wont fall. |
front 241 As the distribution of mass was altered relative to the axis of rotation, the rotation of the object was ________? | back 241 altered. |
front 242 The greater the angular inertia – the harder it is to ? | back 242 to change an objects motion (speed it up or slow it down) |
front 243 Angular inertia: Use knowledge of these principles: | back 243 choke up on an implement to reduce the moment of inertia |
front 244 Explain body position during recovery movements to reduce effort (by reducing inertia) and maximize angular velocity (with sports) | back 244 bring the arm back really close to the body to reduce inertia...like in tennis with back swing and then in recovery phase in swimming...loop arm really close to you. |
front 245 The idea that ______ can alter the rotation of an object with a given moment of inertia is similar to the idea that a linear force can alter the movement of ______? | back 245 torque a mass |
front 246 The angular acceleration of an object is proportional to the net _____ acting on it and inversely proportional to the _____ of the object: explain this? | back 246 torque inertia Greater the force…greater the angular acceleration…greater the inertia…the lower the angular acceleration which shows that the angular acceleration of an object will be greater if the torque is increased or the moment of inertia is decreased |
front 247 We now have a mass moving at an angular velocity, so it has __________, symbol= ? and so we also have to apply an _____ , formula= ? | back 247 angular momentum ‘H’ (although you might also see it as L in physics texts) angular impulse (torque × time, τ·t) |
front 248 The angular impulse–angular momentum relationship would be? What does it basically say? | back 248 τ·t = Iω where a certain impulse creates a change in angular velocity of a certain amount in an object with a given moment of inertia |
front 249 The greater the force… the greater the __________…and the greater the ______…the lower the ____________ | back 249 angular acceleration inertia angular acceleration |
front 250 Most human movements are characterized by a large number of body segments simultaneously moving in _______? | back 250 circles/arcs. |
front 251 For every angular action there is an equal and opposite _______? According to? | back 251 angular reaction As Newton's Third Law states |
front 252 Forces that act to modify motion include (3)? | back 252 Contact Forces Fluid Forces Gravity |
front 253 Normal Reaction | back 253 Contact Forces |
front 254 Buoyancy | back 254 Fluid Forces |
front 255 For every action there is an equal and opposite reaction In terms of forces, the law may be stated as follows: | back 255 Newton’s third law When one body exerts a force on a second body, the second body exerts a “Reaction Force” that is equal in magnitude and opposite in direction on the first body |
front 256 Are forces that occur between objects in contact with each other can be what or what? What are two components that this can be resolved? | back 256 Contact Forces Can be solid or fluid (water & air) |
front 257 Perpendicular to the surface of contact | back 257 Normal Reaction Force vertical Ground Reaction Force |
front 258 Line of action is parallel to the two surfaces in contact and opposes the motion or sliding between the surfaces | back 258 Frictional Force |
front 259 Friction is ______ to the surfaces in contact and _____ the direction of motion ______ component? | back 259 Parallel opposite Usually the horizontal component |
front 260 Frictional force when the object is not moving | back 260 Static friction |
front 261 The maximum static frictional force…friction right before object moves | back 261 Limiting friction |
front 262 If you go over the limiting friction value ________ will occur | back 262 dynamic/kinetic friction |
front 263 The friction between two objects in motion relative to each other | back 263 Dynamic/kinetic friction |
front 264 There are 2 factors that impact the magnitude of friction, explain? | back 264 1. Normal Contact/Reaction Force |
front 265 How much vertical (or perpendicular in relation to motion) pressure there is between the two objects | back 265 Normal Reaction Force |
front 266 The greater the normal reaction force, the greater the overall ? | back 266 friction |
front 267 indicates the relative ease of sliding or the mechanical and molecular interaction between two surfaces in contact Based on the nature of what? | back 267 Coefficient of Friction the surfaces in contact |
front 268 In calculating Friction we must take into consideration these two factors (formula) | back 268 Potential Frictional Reaction Force (PFRF) = |
front 269 Actual FRF will equal the _________ applied, resulting in _________ if they are equal? | back 269 horizontal force no movement |
front 270 example: 100 lb object and coF= 2 PFRF? What happens if you try to move this object with only 50 lbs? With 210 lbs? (what would be the net force and why is there movement) What happens when you bring it back down to 180 lbs? Net force? | back 270 PFRF = 200 lbs Have to overcome the 200 in order to make it move….if you only put in 50 then you will only get 50 back Once horizontal force exceeds the PFRF motion will result : Net force = 10 lbs Once object is moving, if horizontal force is < FRF the object will slow down: Net force = -20 lbs |
front 271 When two components come into contact with one another, the ________ of the objects will influence the behavior of the two objects This definition is for? 2 types? | back 271 elasticity Impact Perfectly Elastic Impact |
front 272 Most impacts are not ? | back 272 “Perfect” |
front 273 describes the relative elasticity of an impact? | back 273 Coefficient of Restitution/Elasticity |
front 274  Previously in lecture you learned that if we know the masses and
velocities of two objects before a collision, we can determine what
their velocities will be afterwards. | back 274 If a ball were to bounce on a concrete floor, its velocity after the
collision should be the same as its velocity before but this isn’t so.
|
front 275 This loss of velocity can be attributed to _________ during the collision. Some energy will be changed to ______ and emitted when? _____ energy is also produced, explain an example? Energy cannot be destroyed but it can be ? | back 275 energy dissipation sound, emitted as the ball hits the ground. Heat -(you might have noticed that a squash ball becomes warmer when it is hit repeatedly before a game). converted to other forms. |
front 276 Coefficient of Restitution aka ? | back 276 CoElasticity |
front 277 Objects _____ slightly as they collide | back 277 deform restitution energy |
front 278 the ability of an object to resist distorting influences and to return to its original size and shape when distorting forces are removed | back 278 Elasticity |
front 279 Whether or not the deformation is permanent depends on the ______ of the interacting objects | back 279 elasticity |
front 280 force that acts to distort | back 280 stress |
front 281 the proportion of distortion that occurs due to stress | back 281 strain |
front 282 Coefficient of Restitution/Elasticity is a term used to compare _________ of different substances | back 282 elasticity |
front 283 Coefficient of Restitution/Elasticity formula? what happens as this calculation approaches one? What happens when a ball of dough is dropped, why? The collision of dough with the floor has a very low ? | back 283 e= square root of (bounce height/ drop height) As CE approaches 1.0 the more perfect the elasticity of an object (returns to normal shape) When a ball of dough hits the floor, it doesn’t undergo restitution, because all its energy is dissipated. coefficient of restitution. |
front 284 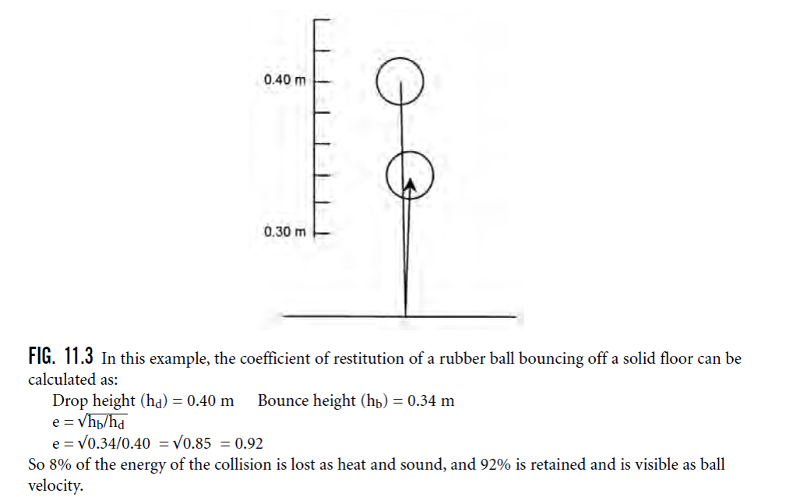 Go over picture? | back 284 pic |
front 285 How much should a basketball be inflated: Basketball should be inflated to rebound to a height of _____- _____ inches at its top when its bottom is dropped from a height of ___ inches | back 285 49 – 54 72 |
front 286 Coefficient of restitution is also affected by what? Give an example? | back 286 temperature. A warm ball will bounce higher than a cold one. |
front 287 Nature of a rebound is governed by: | back 287 Elasticity Mass Velocity Friction Angle |
front 288 An elastic object that strikes the ground obliquely will compress unevenly and rebound at an ______ angle | back 288 oblique |
front 289 Size of the rebound angle compared to striking angle depends upon what 2 things? Describe what a picture of this would look like? | back 289 1. Elasticity of striking object surface line and then perpendicular line straight up and then angle of incidence, and then angle of rebound |
front 290 The rebound of a perfectly elastic object will occur as a ____ angle to the striking angle | back 290 mirror |
front 291 Low coefficients produce angles of reflection greater than ________? | back 291 angle of incidence |
front 292 Coefficient of Restitution/Elasticity | back 292 vertical |
front 293 Friction impacts the _______ component of the rebound. An increase in friction will produce a ______ in angle rebound | back 293 horizontal decrease |
front 294 ____ can influence rebound angles: Topspin causes balls to rebound from horizontal surfaces ____ and with greater ________? Essentially, what does friction do, helping what? | back 294 Spin lower horizontal velocity Goes in the direction the object is moving, helping increase its horizontal rebound velocity |
front 295 Effects of Spin on Rebound: Backspin Essentially, what does friction do, helping what? | back 295 higher slower FRF is in opposite direction as horizontal movement, which slows the object down and helps to give a higher bounce |
front 296 Both _______ and _______ are fluid mediums that exert forces on bodies moving through them. Some will slow _______? Others will provide ? | back 296 air and water movement support or propulsion |
front 297 We often think of liquids when we hear the term ______? | back 297 fluid |
front 298 any substance that tends to flow or continuously deform when acted on by a shear force. Two examples? | back 298 Fluid Gases and liquids |
front 299 The velocity of a body with respect to the velocity of something else, such as the surrounding fluid. Two types? Explain them a little? | back 299 Relative Velocity Absolute vs Relative..important when making comparisons with gender...differences usually decline with relatie |
front 300 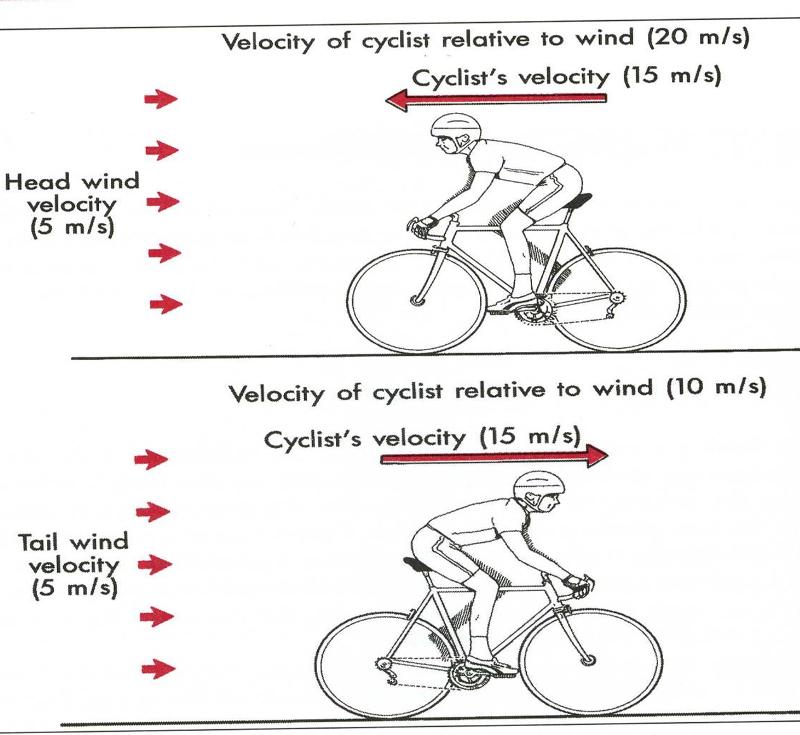 calculate relative velocity? | back 300 Scenario A: (right to left is a neg. velocity)...only going 15 m/s but working harder at 20 m/s....because of the wind Scenario B: working less hard to go at this faster velocity |
front 301 the primary climatic factor in sprint performances. | back 301 Air resistance |
front 302 A strong ______ is very detrimental to performance. But a ______ can improve performances significantly. | back 302 head wind A tail wind |
front 303 What is "wind legal" in running? | back 303 A tail wind can improve performances significantly. |
front 304 Forces produced by gases or liquids: | back 304 1. Buoyancy |
front 305 The __________ a fluid generates is impacted by the properties of the fluid | back 305 magnitude of the forces |
front 306 Ratio of mass/volume | back 306 Density |
front 307 Ratio of weight/volume | back 307 Specific Weight |
front 308 Resistance to fluid flow. | back 308 Viscosity |
front 309 Buoyancy is based on __________ Principle | back 309 Archimedes’ |
front 310 Two things bouyancy is influenced by? What does this mean: More mass concentrated in a given unit of fluid volume at high atmospheric pressures & lower temps | back 310 Influenced by Fluid temperature and Atmospheric Pressure the more dense the fluid medium is |
front 311 Archimedes’ Principle: | back 311 the weight of the liquid displaced |
front 312 If an object exists in a fluid there is a force applied to the object opposite to? | back 312 gravity |
front 313 Buoyancy: The ______ of the force is equal to the _______ of the fluid that the object displaces | back 313 magnitude weight |
front 314 Fb = Vd γ which formula? explain each part? | back 314 Fb = Vd γ |
front 315 For buoyancy: The line of force is applied opposite ______ and passes through the ? | back 315 gravity “center of volume” |
front 316 point around which a body’s volume is equally distributed in all directions | back 316 Center of Volume |
front 317 The heavier the amount of fluid displaced the greater the ? Give an example? Fresh water = ? | back 317 buoyancy force i.e. : in salt water objects produce a greater buoyancy force because salt water weighs more 62.4 lb/ft3 64 lb/ft3 |
front 318  Person = 3 ft3 what is the buoyancy force? Will they float? | back 318 Fresh water: |
front 319 So, why do some people float while others sink? | back 319 Body composition |
front 320 Lift & Drag: Fluid resistance to ? Lift & Drag are the result of either ______ or _______? | back 320 movement fluid movement or object movement |
front 321 Without Lift & Drag what will not occur? | back 321 fluid movement or object movement |
front 322 The resistance to forward motion of an object through a fluid | back 322 Drag |
front 323 Drag is the result of fluid _____ on the leading edge of the object and the amount of __________ (describe this last one) | back 323 pressure turbulence (backward pull on the trailing edge) |
front 324 Produces a suction force pulling the object in the opposite direction of its intended path | back 324 Turbulence |
front 325 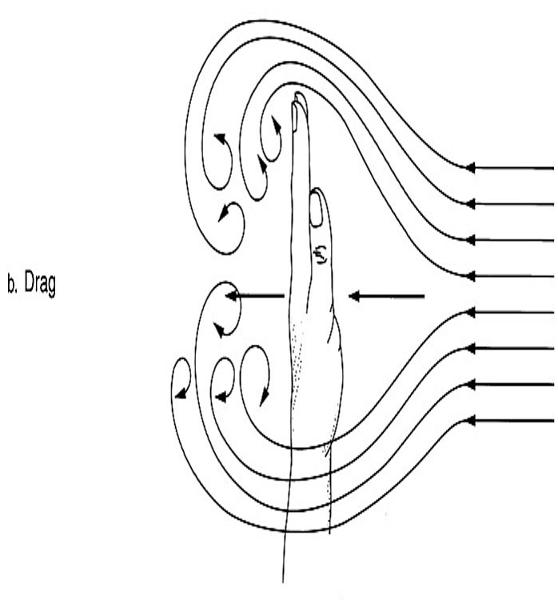 Describe this? | back 325 Hand gets pulled back in the wind when you stick your hand out of the
window |
front 326  Why are these cyclists so close? | back 326 Travel by close….take advantage of forward turbulence flow |
front 327 3 factors Affecting Drag? Describe how they affect drag? With CSA...it is measured _____ to the line of the force? | back 327 1. Viscosity of the fluid Thickness of the fluid 2. Cross sectional area of the object The greater the CSA the greater the drag 3. Velocity of the object or fluid if you double the velocity then you square the drag force=Theoretical Square Law |
front 328 if you double the velocity then you square the drag force | back 328 Theoretical Square Law |
front 329 2 types of drag? | back 329 form and surface drag |
front 330 The _____of the object makes the fluid unable to follow the contours of the object causing ________? What type of drag is this? | back 330 shape turbulence Form Drag |
front 331 A row boat vs a kayak dealing with aerodynamics? | back 331 A lot of work in a row boat |
front 332 The friction that exists between the boundary layer and the object | back 332 surface drag |
front 333 the layer of fluid directly next to the object | back 333 Boundary layer |
front 334 smooth, unbroken fluid flow | back 334 Laminar flow |
front 335 Advantage of tight clothes and shaving in relation to surface drag? | back 335 Can decrease surface drag & enhance laminar flow by shaving, high-tech fabrics, etc |
front 336 a force generated by the changes in fluid pressure as the result of different fluid velocities | back 336 lift |
front 337 __________ Principle: | back 337 Bernoulli’s increases less differences on either side Airplane wing (airfoil shape) |
front 338 Slower moving means _____ pressure which generates ____? With lower pressure what is the speed like? | back 338 Higher Pressure Faster moving |
front 339 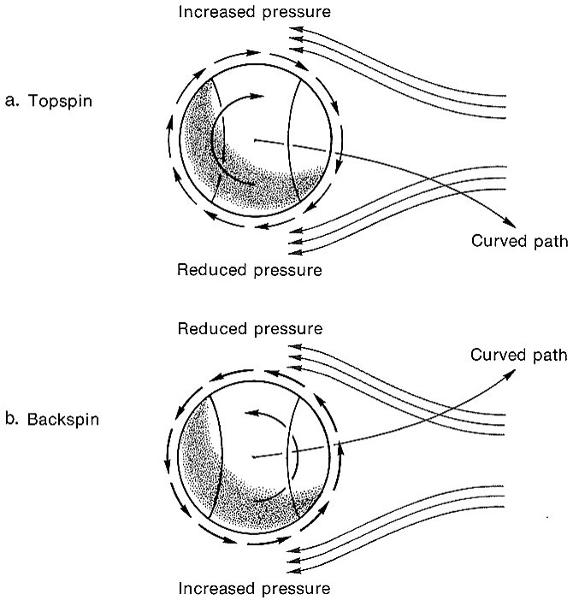 LIFT : with Topspin & Backspin? | back 339 with topspin: increased pressure on top which means slower movement and reduced pressure on bottom meaning increased speed going around the ball in a clockwise manner....topspin brings the ball down with backspin: increased pressure on bottom meaning slower speed and reduced pressure on top meaning faster speed...increased speed going around the ball in a counter clockwise manner bringing the ball backwards |
front 340 So, why does a golf ball have dimples? | back 340 Reduces turbulent flow on back end of it…making it able to fly forward |