Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
IGCSE Maths
front 1 Find the HCF | back 1 Use tree diagram to find the product of prime numbers, (do factors and when prime number circle it) multiply the common ones from each number. |
front 2 Find the LCM | back 2 Use tree diagram to do prime factorisation then multiply all the ones together without repeating from both numbers. |
front 3 Recurring decimal to fraction | back 3 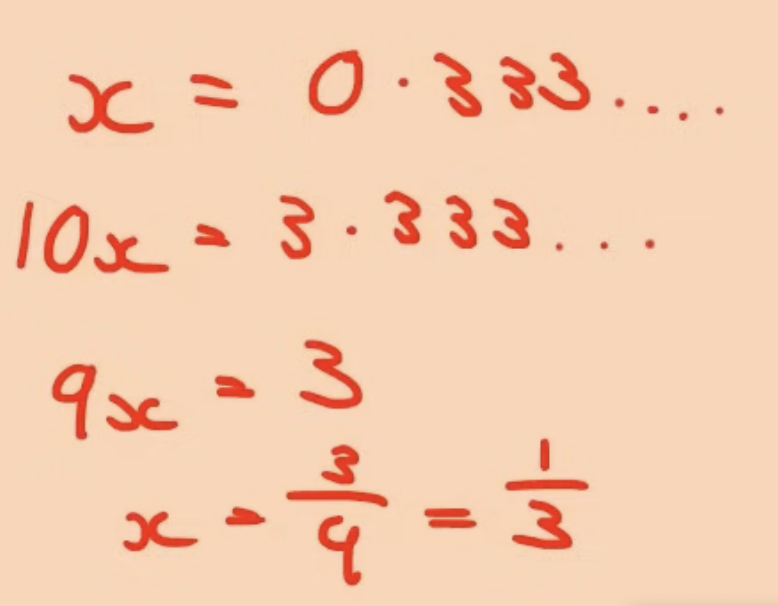 write x = recurring decimal, times both sides by ten. then take away 1x to remove the recurring decimal numbers and be left with the whole number. then simplify. |
front 4 natural numbers | back 4 positive whole numbers, starting from 1. |
front 5 integers | back 5 whole numbers (positive, zero and negative) |
front 6 rational and irrational numbers | back 6 Rational numbers can be expressed as a fraction where both sides are integers, but irrational numbers can't. |
front 7 reciprocal | back 7 a number that is found by dividing 1 by that number |
front 8 ∈ | back 8 element is in set |
front 9 ∉ | back 9 element isn't in set |
front 10 ∅ | back 10 The empty set |
front 11 A ⊆ B | back 11 A is a subset of B |
front 12 A ⊈ B | back 12 A is not a subset of B |
front 13 A ∪ B | back 13 all elements that are in either set A, or set B, or both |
front 14 A ∩ B | back 14 The elements in both sets, intersection of Venn diagram |
front 15 recall of squares and their corresponding roots from 1 to 15 | back 15 1 = 12 4 = 22 9 = 32 16 = 42 25 = 52 36 = 62 49 = 72 64 = 82 81 = 92 100 = 102 121 = 112 144 = 122 169 = 132 196 = 142 225 = 152 |
front 16 recall cubes from 1 to 15 | back 16 1 = 13 8 = 23 27 = 33 64 = 43 125 = 53 216 = 63 343 = 73 512 = 83 729 = 93 1000 = 103 |
front 17 What are the 6 laws of indices? 7 | back 17
|
front 18 Simple interest | back 18 PRT/ 100 principal (original amount) x interest rate x time / 100 |
front 19 Compound interest | back 19 P(1 + r/100)n Principal( 1 + rate/100)number of years |
front 20 Exponential growth and decay | back 20 P(1+r)n and. P(1-r)n principal (original amount) (1+rate)number of years etc. |
front 21 Frequency density | back 21 Frequency / class width |
front 22 Acceleration | back 22 Speed difference / time |
front 23 Area of sector of a circle and sector length | back 23 area = (percentage of circumference x area of circle) xo /360 x π x r2 Sector length = (percentage of circumference x circumference ) x0 / 360 x 2π x r |
front 24 Circle theorems | back 24 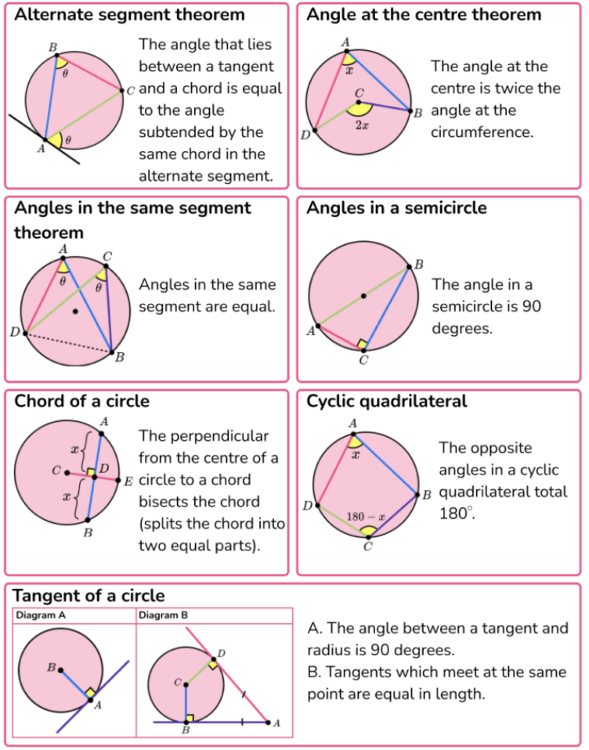 |
front 25 How to do differentiation and the notation that stands for it | back 25  The original formula only tells you the amount
(height, profit, distance, etc.) at a point. dy/dx |
front 26 Different types of curves based off equations | back 26  |
front 27 Calculate percentage increase or decrease. | back 27  Value change / initial value x 100 |
front 28 Calculate using reverse percentages | back 28
|
front 29 Rationalise the denominator. | back 29 You remove any square roots (surds) from the denominator by multiplying the entire fraction (numerator and denominator) by the surd in the denominator. For denominators with a sum or difference of surds (e.g., a + b√c), you multiply by the same expression with the opposite sign (the conjugate) to use the difference of squares formula (a² - b²) and eliminate the surd. Example with a rational number and a surd e.g., 1 / (√5 + √2)
|
front 30 how to solve quadratic simultaneous equations | back 30 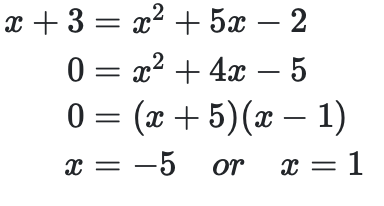 When don't know value of y: For y = x + 3 and y = x2 + 5x -2 Then once have x sub and find y. 2 answers for quadratic equation. When know: multiply equation to make coefficients the same. then take them away for each other to find one value. sub this value into the original to find the other. 2x + 2y = 6 from 2x + 3y = 7 would result in (2x - 2x) + (3y - 2y) = 7 - 6, or y = 1 |
front 31 how to solve regular simultaneous equations | back 31 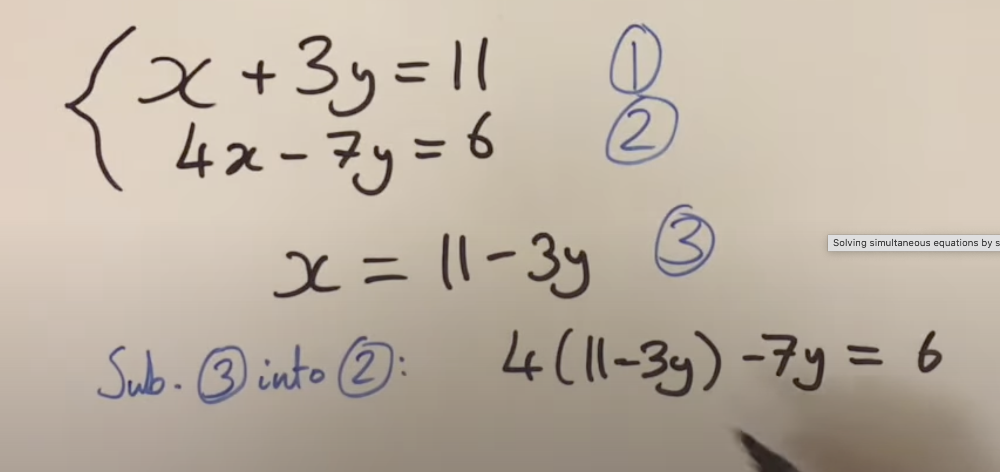 1. Find x or y 2. sub into other equation 3. solve |
front 32 rules for linear equality graphs. | back 32 Broken lines are used to represent greater or lesser than but not equal (<, >) and straight lines for greater or lesser and equal (⩽, ⩾). shading is used to represent unwanted regions |
front 33 How to identify and solve linear, quadratic, cubic and exponential sequences. | back 33 Exponential sequences increase by a common ratio from term to term, with the nth term being defined as a × r(n−1) where a is the first term and r is the value that you multiply by each time. Patterns in linear sequences are recognizsd by identifying a constant difference between consecutive terms. First part is difference x n and then figure out what you have to add or minus to make it correct. For quadratic (nth term = an2 + bn + c ) equal second difference) The coefficient of the n2 term of a quadratic sequence is half of the second difference. Then subtract this from the original sequence and you will have a regular linear equation to solve and make up the rest of the equation. For cubic (equal third difference) nth term = an3 + bn2 + cn + d first find the third difference. The coefficient for the n3 term is the third difference divided by 6. Take this away and you will be left with a quadratic equation and second difference, solve this for the n2 coefficient and subtract. Then solve the linear and put it together. |
front 34 graphs for sin, cos and tan and finding other solutions | back 34  |
front 35 Express direct and inverse proportion in algebraic terms | back 35 ∝ is symbol for proportion. k is used for the constant. Direct proportion = a∝ kb Inverse proportion = The statement a is inversely proportional to b is written: a ∝ 1/b then to solve replace 1 with the constant. |
front 36 how to calculate Gradient | back 36 Gradient = rise ÷ run (or change in y ÷ change in x) |
front 37 For a quadratic function how to sketch a graph and find turning point. | back 37 If coefficient of x2 is positive, the graph will be a positive U-shaped curve and vice versa. Find y and x intercepts by making x and y 0 in the equation. Find the turning point by either: using the equation x = -b/2a from the equation. This gives x and to find y sub value of x in original equation. If a is positive it is a min point, and if negative then max point. The original equation is y = ax2 + bx + c. or complete the square to form a(x+p)2 + q where the coordinate are (-p, q) |
front 38 How to complete the square | back 38 y = ax2 + bx + c style equation. say for y = x2 - 8x + 13. Half the b quantity (-8) and make a bracket (x - 4)2 this makes everything match the above equation but the -42 = 16 which needs 3 take off it to become 13. so the final equation is (x - 4)2 - 3 |
front 39 For a recipricoral function how to sketch a graph and find the asymptotes | back 39 standard form equation is y = a/x + q when a is negative the graph will be top left and bottom right and vice versa. The graph will intercept x if q is not equal to 0. To find the x intercept make y = 0 and find for x in the above equation. One asymptote is the y axis and the other is equal to y = q |
front 40 maxima and minima and stationary points on a cubic graph | back 40  at stationary point dy / dx = 0 so differentiate the equation to find its new version and sub y for zero to find the values for x. |
front 41 how to find stationary points on a cubic graph | back 41  at stationary point dy / dx = 0 so differentiate the equation to find its new version and sub y for zero to find the values for x. then sub x into original equation to find y. |
front 42 second differential when finding max and min points on a cubic graph | back 42  first differentiate once, then do it a second time to find the new equation. Into the new equation sub the stationary point value for x and if it is positive it is the minimum point. The function for differentiating twice is d2y / (dx)2 . |
front 43 order of composite functions | back 43 if gf(x) then find for f first then g. for a function the domain is anything that can become x and the range is what the answer range can be. |
front 44 how to find difference of a line segment and the midpoint of a line segment | back 44  the midpoint is found by finding the mean of x and y. add the x coordinates together and divide by 2 to find the new x coordinate and same for y. |
front 45 how to find the equation of a perpendicular bisector of a line | back 45 First find the midpoint of the line the (midpoint is found by finding the mean of x and y). Then find the slope of the line with the formula y2 - y1 / x2 - x1 . To find the gradient of the bisecting line calculate the negative reciprocal (when you swap numerator and denominator) so 3/2 becomes -2/3. Sub all this into the y = mx + c formula. we have the gradient and the x and y coordinates of the point it goes through. and solve to find c. then you have the entire equation. |
front 46 Find the gradient and equation of a straight line parallel | back 46 The gradient is the same as they are parallel and you are given the x and y coordinates it passes through. Sub all this into the y = mx + c formula. (the gradient and the x and y coordinates) and solve to find c. then you have the entire equation. |
front 47 acute, obtuse and reflex angles | back 47 Acute - below 90 Obtuse - between 90 and 180 Reflex - between 180 and 360 |
front 48 similar vs congruent | back 48 Congruent shapes are identical in both shape and size, meaning one can be perfectly superimposed on the other, while similar shapes have the same shape but can differ in size. |
front 49 rhombus • parallelogram • trapezium. | back 49  Rhombus All four sides are of equal length, Both pairs of opposite sides are parallel, Opposite angles are equal, and It is a type of parallelogram. Parallelogram
Trapezium (Trapezoid) Has four sides, Has exactly one pair of parallel sides, and The non-parallel sides are called legs. |
front 50 prism and cuboid | back 50  a 3D shape with two identical, parallel ends (the bases) and a constant cross-section throughout its length a cubbies is any 3d shape with 6 faces like a cube but it can be a rectangle etc. |
front 51 frustum | back 51  the shape created when the top part of a cone or pyramid is cut off by a plane parallel to its base, leaving a solid with two parallel bases |
front 52 parts of circle • chord • major and minor arc • sector • segment. | back 52  |
front 53 Draw nets. cubes, cuboids, prisms and pyramids | back 53  For a cylinder : The length of the rectangle is equal to the circumference of the circles. The width of the rectangle is equal to the height of the cylinder. For a pyramid : The perpendicular height of each triangle is equal to the slant height of the pyramid. |
front 54 The relationship of similar shapes lengths, surface areas and volumes of similar solids. | back 54 k is used to depict scale scale factor. Lengths are related by the scale factor (k), areas by k², and volumes by k³. k = length A / length B k2 = area A / area B k3 = volume A / Volume B and when converting between them. |
front 55 how to calculate the sum of interior angles on a polygon and therefore each individual angle | back 55 For any polygon with n sides, the sum of its interior angles is calculated with the formula (n - 2) × 180°. For a regular polygon, you can then find each interior angle by dividing the sum by n. |
front 56 m3 to L | back 56 1m3 = 1000L same as ml |
front 57 find the surface area and volume of a frustum. | back 57 V = (πh/3)(R² + Rr + r²), where h is the height, R is the radius of the larger base, and r is the radius of the smaller base. The total surface area is the sum of the areas of the two circular bases and the curved lateral surface: A = πL(R + r) + πR² + πr², where L is the slant height. |
front 58 The ambiguous case | back 58 The ambiguous case is identified when the side opposite the known angle is shorter than the other known side. This means it can swing like a pendulum and form 2 triangles so there are 2 possible answers for the angle you are finding. The ambiguous case, which can arise when using the sine rule with two sides and a non-included angle, requires checking for two possible solutions for an angle, one acute and one obtuse, by considering their sum with the given angle. |
front 59 Calculate the magnitude of a vector | back 59  |
front 60 For a vector if given A and B find AB | back 60  To find PQ P subtract the values of the coordinates of from the coordinates of Q because you start at P and want to get to Q. |
front 61 show that 3 points are collinear | back 61  |
front 62 show that vectors are parallel | back 62 Vectors are parallel if one is a scaler multiple of each other. eg A = k x B with k being the multiple. similar to collinear but this is between three points. |
front 63 sample space | back 63  |
front 64 two-way tables | back 64  |
front 65 Identify the modal class from a grouped frequency distribution. | back 65 find the class interval with the highest frequency. |
front 66 Estimate and interpret the median, percentiles, quartiles and interquartile range from cumulative frequency diagrams. | back 66 A horizontal line is drawn from the calculated median, Q1 or Q3 position on the cumulative frequency (y-axis) to intersect the cumulative frequency curve. |
front 67 Calculate with frequency density on a histogram | back 67 On histograms, the vertical axis is labelled ‘Frequency density’. frequency density = frequency ÷ class width. |
front 68 When you know two sides and the included angle calculate area of triangle | back 68 Area = ½ * a * b * sin(C)
|
front 69 area of trapezium | back 69 1/2 x (upper length + lower length) x height |