Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
Chapter 1 Early Transcendentals
front 1 If f(x) = 3x + 1nx, find f-1(3) | back 1 1 |
front 2 Solve each equation for x a) 1nx = 4 b)eex = 2 | back 2 x = e4, x = ln(ln 2) |
front 3 Simplify the expression sin (2cos-14x) | back 3 8x√1-16x2 |
front 4 Fill in the blanks Let f(x) = 5 + x2 + tan(πx/2), where -1 < x < 1 | back 4 5,3 |
front 5 Determine whether f is even, odd, or neither f(x) = 8x2/x4 + 1 | back 5 even |
front 6 Find the range of the function h(x) = √4 - x2 | back 6 0 ≤ h(x) ≤ 2 |
front 7 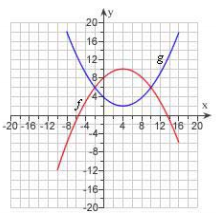 The graphs of f(x) and g(x)are given. | back 7 a) -2, 10 |
front 8 A spherical balloon with radius r inches has volume 4/3 πr. | back 8 4/3 π(3r2 + 3r + 1) |
front 9 It makes sense that the larger the area of a region, the larger the
number of species that inhabit the region. Many ecologists have
modeled the species-area relation with a power function and, in
particular, the number of species S of bats living in caves in central
Mexico has been related to the surface area A measured in
m2 of the caves by the equation S = 0.7A03
| back 9 a) 3 species |
front 10 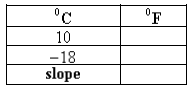 The relationship between the Fahrenheit and Celsius temperature scales is given by the linear function. F = 9/5 C + 32 Complete the table and find the slope. | back 10 (10,50)(-18,0);slope = 2 |
front 11 Plot the graph of the function in (a) the standard viewing window and (b) the indicated window f(x) = x√7-x4, [-3, 3] X [-5,5] | back 11 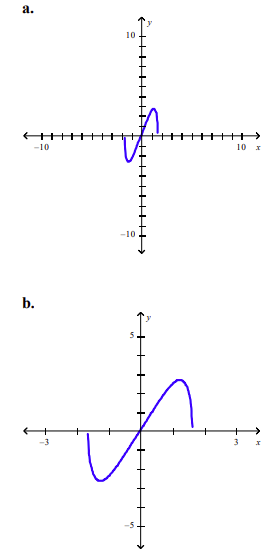 |
front 12 Plot the graph of the function f in an appropriate viewing window. f(x) = 2x3 - 5x2 + 4x + 27 | back 12 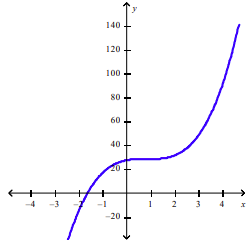 |
front 13 Find the points of intersection of the graphs of the functions. Express your answers accurate to five decimal places. f(x) = 0.3x2 - 1.1x - 3.5; g(x) = -0.2x2 + 0.4x + 6.9 | back 13 (-3.30104, 3.40021), (6.30104, 1.47979) |
front 14 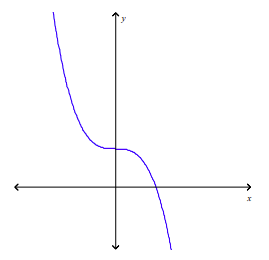 Determine whether f is one-to-one. | back 14 Yes |
front 15 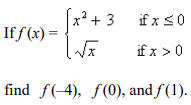 | back 15 f(-4) = 19, f(0) = 3, f(1) = 1 |
front 16 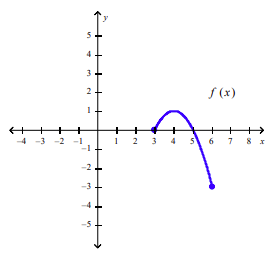 Refer to the graph of the function f in the following figure. a. Find f (3). | back 16 a. 0 |
front 17 Let f(x) = x2 -6x + 7 and g(x) = √x+3, Find (g ⚬ f)(9) | back 17 √37 |
front 18 Find f ⚬ g ⚬ h if f(x) = √x, g(x) = 7x + 4, and h(x) x2 - 4 | back 18 √7x2-24 |
front 19 Let f(x) = x2 - 18x + 75 and g(x) = √x+7. Find (f ⚬ g)(74)(g ⚬ g)(74) | back 19 -6 |
front 20 Find the function g such that h(x) = (g ⚬ f)(x) h(x) = sin5x and f(x) = sin x | back 20 g(x) = x5 |
front 21 Find all solutions of the equation correct to two decimal places. √x = x3 - 4 | back 21 1.75 |
front 22 Solve each equation for x a) ln x = 6 | back 22 x = e6, x = ln(ln 2) |
front 23 Find the exact value of the expression. tan(arcsin 1/2} | back 23 √3/3 |
front 24 Find the range of the function h(x) = √25-x2 | back 24 0≤h(x)≤5 |
front 25 Express the function in the form of f ⚬ g ⚬ h H(x) = 3 - 6x3 | back 25 h(x) = x3, g(x) = 6x, f(x) = 3 - x |
front 26 Plot the graph of the function f in an appropriate viewing window.
| back 26 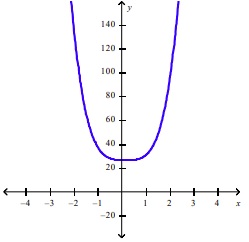 |
front 27 Find the points of intersection of the graphs of the functions.
Express your answers accurate to five decimal places. | back 27 (–3.22169, 3.57981), (6.02169, 0.25219) |
front 28 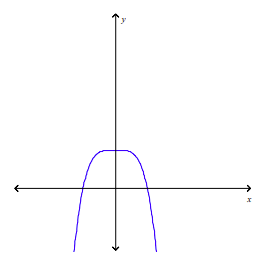 Determine whether f is one-to-one. | back 28 No |
front 29 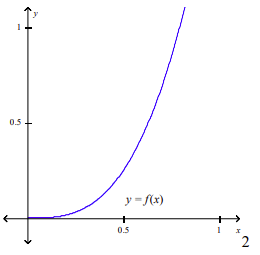 The graph of f is given. Sketch the graph of f-1 on the same set of axes. | back 29 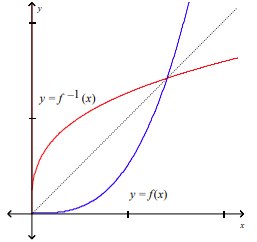 |
front 30 Find the inverse of f. Then sketch the graphs of f and f-1 on the same set of axes. f(x) = cos-1(x/2), -2≤x≤2 | back 30 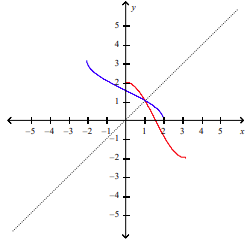 f-1(x) = 2cos x, 0 ≤ x ≤ π |
front 31 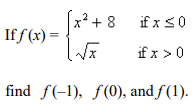 | back 31 f(-1) = 9, f(0) = 8, f(1) = 1 |
front 32 Refer to the graph of the function f in the following figure. a. Find f(0). | back 32 a. 0 |
front 33 Determine whether the function is even, odd, or neither. f(x) = 2x2 + 9x | back 33 Neither |
front 34 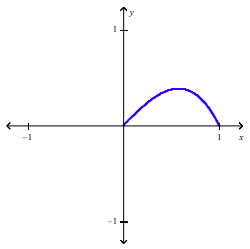 The following figure shows a portion of the graph of a function f defined on the interval [-1,1]. Sketch the complete graph of f if it is known f is odd. | back 34 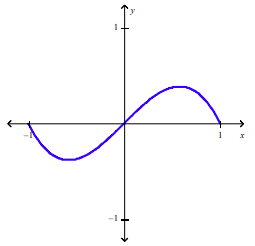 |
front 35 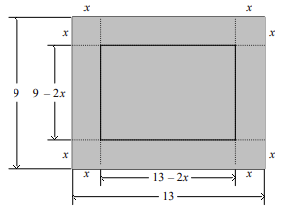 By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box can be made. If the cardboard is 13 in. long and 9 in. wide and the square cutaways have dimensions of x in. by x in., find a function that gives the volume of the resulting box. | back 35 V = 4x3 - 44x2 + 117x |
front 36 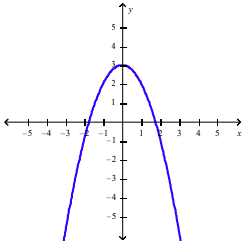 Use the vertical line test to determine whether the curve is the graph of a function of x. | back 36 Yes |
front 37 Let f(x) = x2 - 18x + 80 and g(x) = √x+2. Find (g ⚬ f)(17) | back 37 √65 |
front 38 Find f ⚬ g ⚬ h if f(x) = x-1/x+1, g(x) = 4√x, and h(x) = x + 1 | back 38 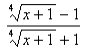 |
front 39 Let f(x) = x2 - 14x + 38 and g(x) = √x+12. Find (f ⚬ f)(10)(g ⚬ g)(13) | back 39 70 |
front 40 Find the function g such that h(x) = (g ⚬ f)(x). h(x) = 1/6x-5 and f(x) = 6x-5 | back 40 g(x) = 1/x |
front 41 Find the points of intersection of the graphs of the functions.
Express your answers accurate to five decimal places. a. (–0.55126, –5.84352), | back 41 d |
front 42 Starting with the graph of y = ex, find the equation of the graph that results from reflecting about the line y = 3. a. y = -ex | back 42 b |
front 43 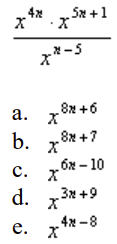 Use the Law of Exponents to rewrite and simplify the expression. | back 43 a |
front 44 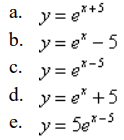 Starting with the graph of y = ex, write the equation of the graph that results from shifting 5 units right. | back 44 c |
front 45 Suppose that the graph of y = log3x is drawn on a
coordinate grid where the unit of measurement is an inch. How many
miles to the right of the origin do we have to move before the height
of the curve reaches 2 ft? Rounded to the nearest mile. | back 45 b |
front 46 Find the exact value of the given expression. | back 46 b |
front 47 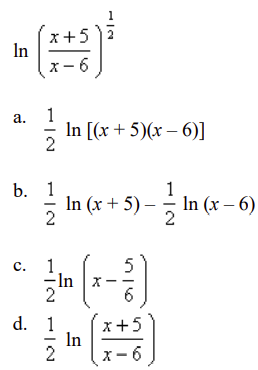 Use the laws of logarithms to expand the expression. | back 47 b |
front 48 Simplify the expression. e3ln6 a. 9 | back 48 c |
front 49 Find a formula for the inverse of the function. y = ln(x + 6) a. y = ex - 6 | back 49 a |
front 50 Find the exact value of the expression. log5100 + log525 - 2log52 a. 7 | back 50 d |
front 51 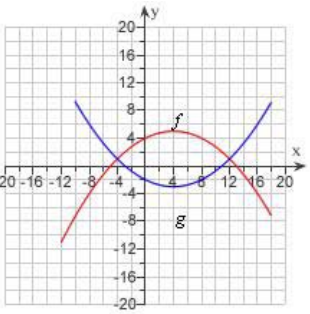 The graphs of f(x) and g(x) are given. For what values of x is f(x) = g(x)? | back 51 e |
front 52 Which of the following graphs is neither even nor odd? | back 52 b |
front 53 A rectangle has perimeter 14m. Express the area of the rectangle as a
function A(l) of the length of one of its sides. | back 53 a |
front 54 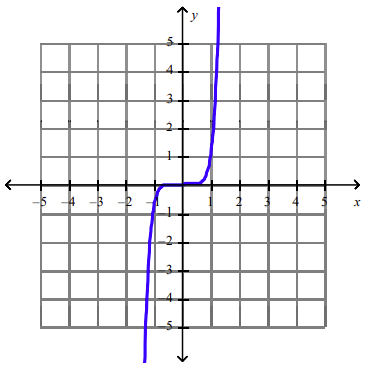 What is the equation of this graph? a. y = x8 | back 54 e |
front 55 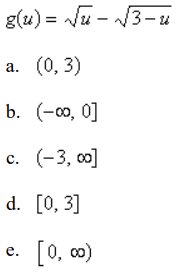 Find the domain | back 55 d |
front 56 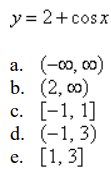 Find the range of the function | back 56 e |
front 57 The relationship between the Fahrenheit and Celsius temperature scales is given by the linear function. F = 9/5 C + 32 What is the F-intercept and what does it represent a. 9/5, Fahrenheit temperature corresponding to 0°C | back 57 e |
front 58 If f(x) = x + 5 and h(x) = 4x - 10, find a function g such that g ⚬ f
= h. | back 58 d |
front 59 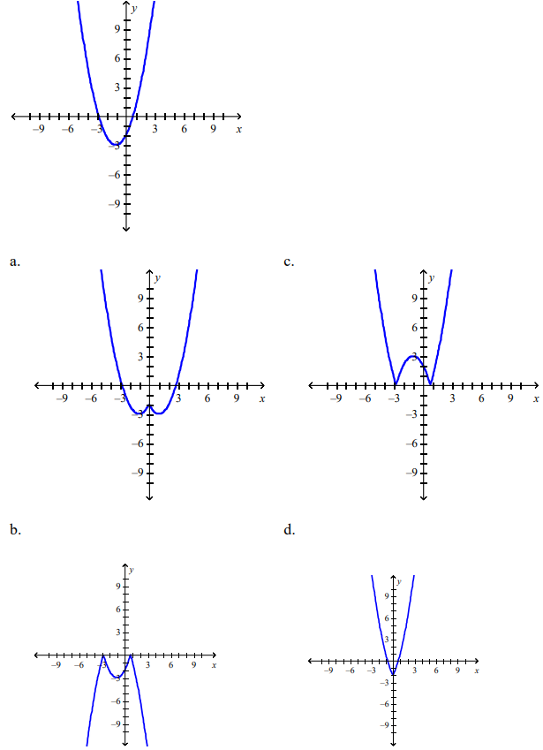 The graph of the function f follows. Choose the graph of y = f(|x|) | back 59 d |
front 60 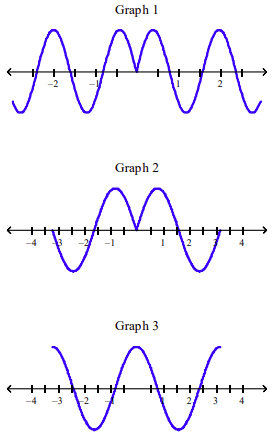 Which of the following graphs is the graph of the function? f(x) = sin |2x| a. Graph 2 | back 60 a |
front 61 Find all solutions of the equation correct to two decimal places. x3 - 9x2 - 100 = 0 a. x = 10 | back 61 a |
front 62 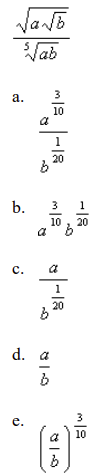 Use the Law of Exponents to rewrite and simplify the expression. | back 62 b |
front 63 Starting with the graph of y = ex, write the equation of
the graph that results from shifting 3 units right. | back 63 e |
front 64 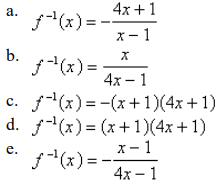 Find the inverse function of f(x) = x+1/4x+1 | back 64 e |
front 65 Find f-1(a) for the function f and the real number a. f(x) = x3 + x - 3; a = -1 a. 2 | back 65 b |
front 66 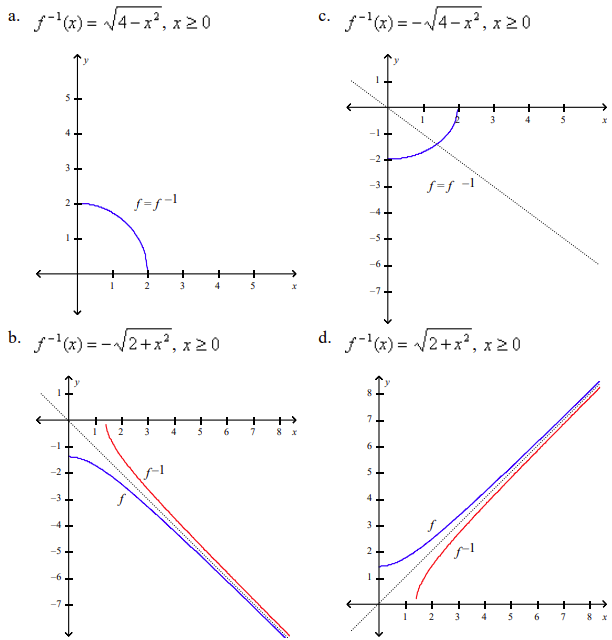 Find the inverse of f. Then sketch the graphs of f and f-1 on the same set of axes. f(x) = √4-x2, x ≥ 0 | back 66 a |
front 67 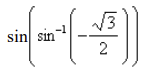 Find the exact value of the given expression a. -1/2 | back 67 b |
front 68 Simplify the expression. e2ln6 a. 12 | back 68 c |
front 69 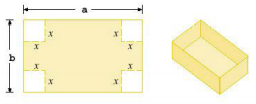 A box with an open top is to be constructed from a rectangular piece of card board with dimensions b = 9 in. by a = 24 in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. | back 69 b |
front 70 A rectangle has perimeter 22m. Express the area of the rectangle as a
function A(l) of the length l of one of its sides. | back 70 d |
front 71 If f(x) = 4x2 + 2, find and simplify f(1+h)-f(1)/h , where
h ≠ 0. | back 71 d |
front 72 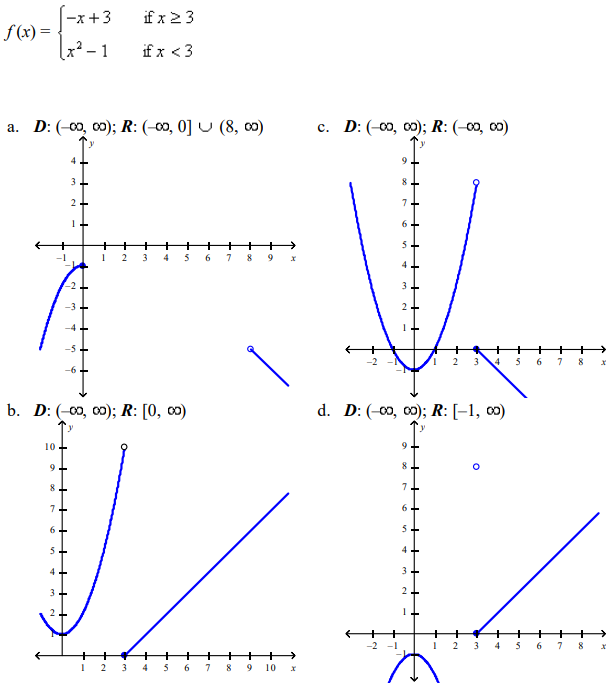 Find the domain and sketch the graph of the function. What is its range? | back 72 c |
front 73 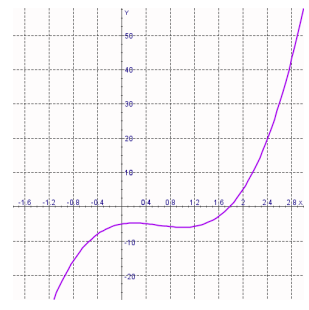 The graph of the function f is given. State the value of f(0).
| back 73 d |
front 74 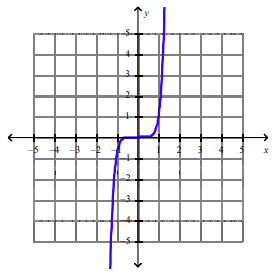 What is the equation of this graph? | back 74 c |
front 75 The relationship between the Fahrenheit and Celsius temperature scales is given by the linear function. F = 9/5 C + 32 What is the F-intercept and what does it represent? | back 75 e |
front 76 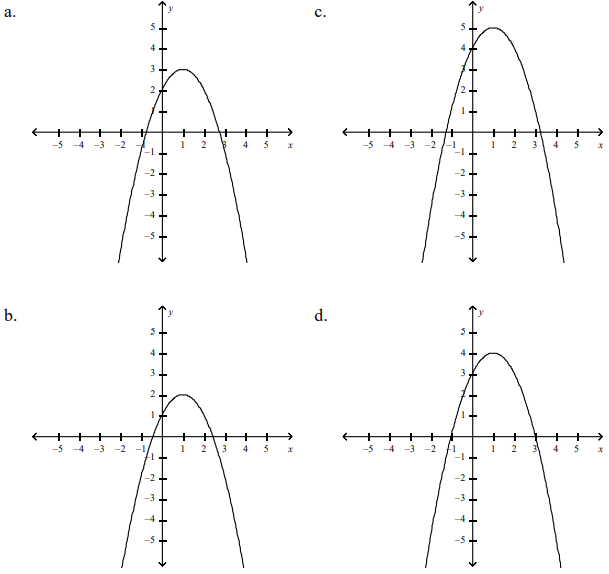 Graph the function by hand, not by plotting points, but by starting with the graph of one of the standard functions and then applying the appropriate transformations. y = 1 + 2x - x2 | back 76 b |
front 77 Suppose that the graph f is given. Describe how the graph of the
function y = f(x - 3) - 3 can be obtained from the graph of f.
| back 77 a |
front 78 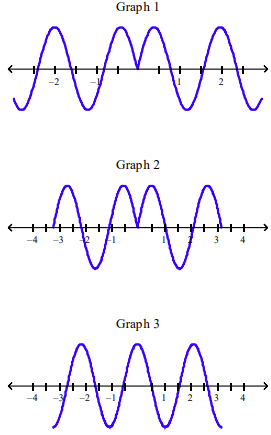 Which of the following graphs is the graph of the function? f(x) = sin |3x| a. Graph 3 | back 78 c |
front 79 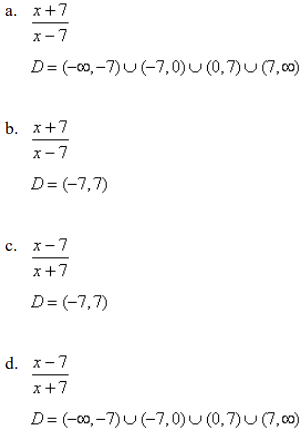 Find the function f/g and its domain if f(x) = x/x-7 and g(x) = x/x+7. | back 79 a |
front 80 The graph of the function f(x) = x2 - 9x + 5 has been
compressed horizontally by a factor of 2. Find the function for the
transformed graph. | back 80 a |
front 81 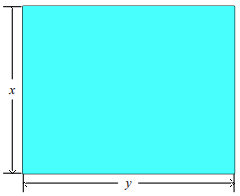 Sandy wishes to have a rectangular garden in her backyard. She has 40
ft of fencing with which to enclose her garden. Letting x denote the
width of the garden, find a function f in the variable x that gives
the area of the garden. Select the correct answer. | back 81 b |
front 82 An open rectangular box with volume 2m3 has a square base. Express the surface area of the box as a function S(x) of the length x of a side of the base. | back 82 S(x) = x2 + 8/x |
front 83 Determine whether f is even, odd, or neither. Select the correct answer. f(x) = 4x2/x4+5 a. neither | back 83 c |
front 84 The monthly cost of driving a car depends on the number of miles driven. Julia found that in October it cost her $200 to drive 300mi and in July it cost her $350 to drive 600mi. Express the monthly cost C as a function of the distance driven d assuming that a linear relationship gives a suitable model. | back 84 C = 0.5d + 50 |
front 85 If f(x) = x + 5 and h(x) = 4x - 10, find a function g such that g ⚬ f = h. | back 85 g(x) = 4x - 30 |
front 86 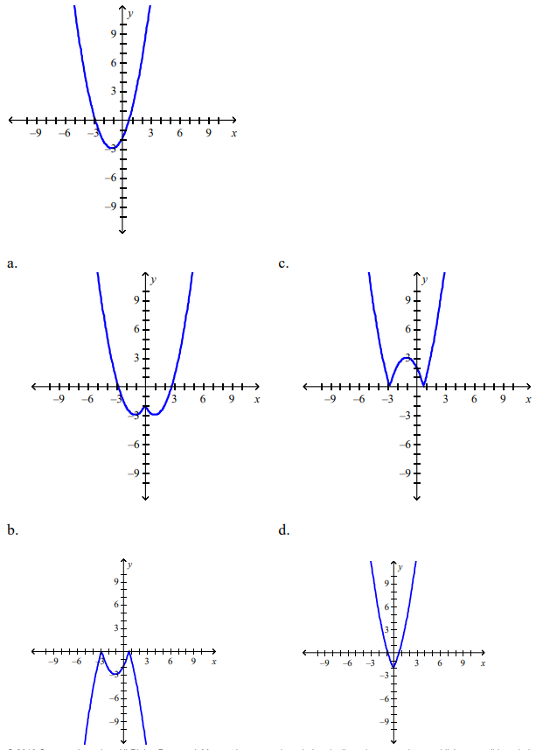 The graph of the function f follows. Choose the graph of y = f(|x|) | back 86 d |
front 87 Sketch the graph of y = -1 - cos x over one period. | back 87 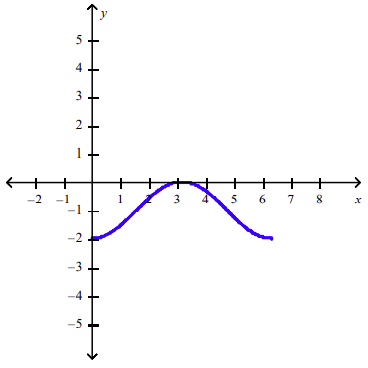 |
front 88 Find the function f g and its domain if f(x) = √x+7 and g(x) = √x-7 . | back 88 √x2-49 |
front 89 If a ball is thrown into the air with a velocity of 58ft/s, its height (in feet) after t seconds is given by H = 58t - 9t2 Find the velocity when t = 9. Select the correct answer.
| back 89 b |
front 90 The position of a car is given by the values in the following table. t (seconds) 0, 1, 2, 3, 4 Find the average velocity for the time period beginning when t = 2 and lasting 2 seconds. | back 90 33.2 ft/s |
front 91 Find the value of limx→0+ f(x). Select the correct answer. f(x) = 1/1+61/x a. 0 | back 91 a |
front 92 Find the vertical asymptotes of the function. y = 8x2+1/9x-8x2 | back 92 none of these |
front 93 Find the limit limk→3 (h4 - 3h3 - 4h + 5) | back 93 -7 |
front 94 Find the limit limx→1 x2+x-2/x-1, if it exists.
Select the correct answer. | back 94 b |
front 95 Evaluate the limit, if it exists. limk→0 (x-h)6-x6/h | back 95 -6x5 |
front 96 Find the limit. limx→2- x2-2x/x2-4x+4 | back 96 -∞ |
front 97 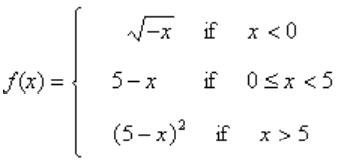 Determine where f is discontinuous. | back 97 0 and 5 |
front 98 If f and g are continuous functions with f(9) = 6 and limx→9 [2f(x) - g(x)] = 9, find g(9). a. g(9) = 21 | back 98 e |
front 99 How would you define f(7) in order to make f continuous at 7? f(x) = x2-2x-3/x-7 | back 99 f(7) = 12 |
front 100 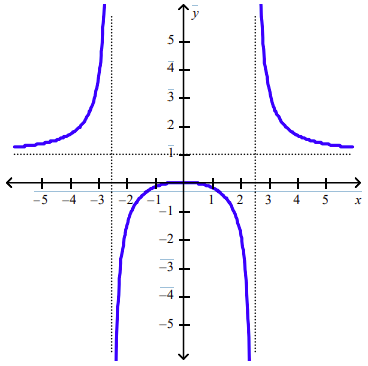 Use the graph to determine where the function is discontinuous. a. At 0 | back 100 c |
front 101 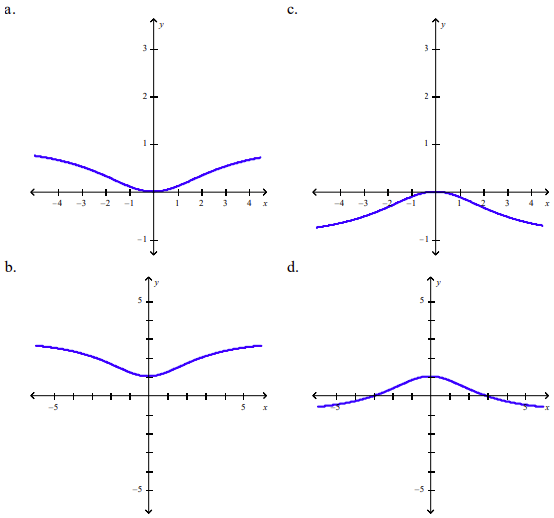 Plot the graph of the function f in an appropriate viewing window. Select the correct answer. f(x) - x2/x2+8 | back 101 a |
front 102 Plot the graph of the function f in an appropriate viewing window. f(x) = x + 0.02 sin 40x | back 102 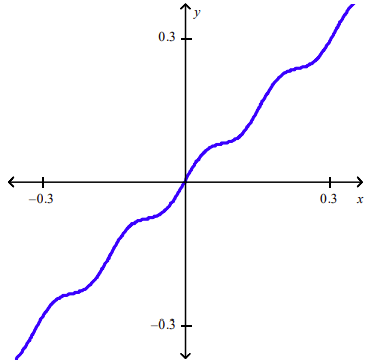 |
front 103 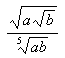 Use the Law of Exponents to rewrite and simplify the expression. | back 103 a3/10b1/20 |
front 104 Starting with the graph of y = ex, find the equation of
the graph that results from reflecting about the line y = 3. Select
the correct answer. | back 104 b |
front 105 Use the Law of Exponents to rewrite and simplify the expression. x4nx5n+1/xn-5 | back 105 x8n + 6 |
front 106 Starting with the graph of y = ex, write the equation of
the graph that results from shifting 5 units right. Select the correct
answer. | back 106 c |
front 107 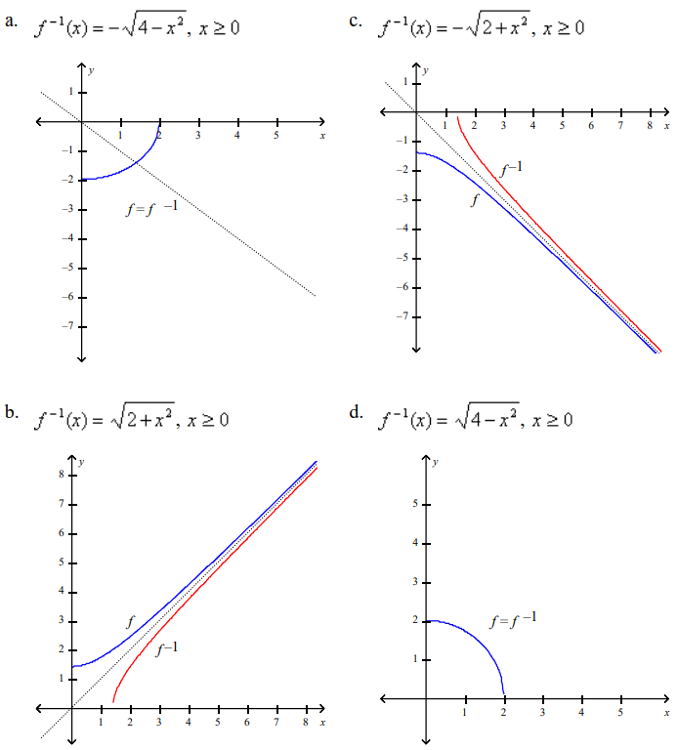 Find the inverse of f. Then sketch the graphs of f and f-1
on the same set of axes. f(x) = √4-x2, x ≥ 0 | back 107 d |
front 108 Solve the equation. 4ex + 5 = 2 | back 108 x = ln 1/2 - 5 |
front 109 When a camera flash goes off, the batteries immediately begin to recharge the flash's capacitor, which stores electric charge given by Q(t) = Q0(1 - e-tla) (The maximum charge capacity is Q0 and t is measured in seconds.) How long does it take to recharge the capacitor to 90% of capacity if a = 3? | back 109 -3ln(1/10) seconds |
front 110 If f(x) = x2 - x + 6, evaluate the difference quotient f(a+h)-f(a)/h.
Select the correct answer. | back 110 e |
front 111 A rectangle has perimeter 14m. Express the area of the rectangle as a function A(l) of the length l of one of its sides. | back 111 A(l) = 7l - l2 |
front 112 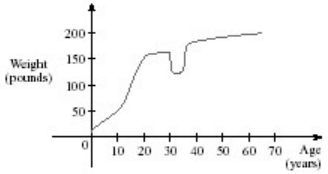 The graph shown gives the weight of a certain person as a function of age. Find the age at which the person started an exercise program. | back 112 30 |
front 113 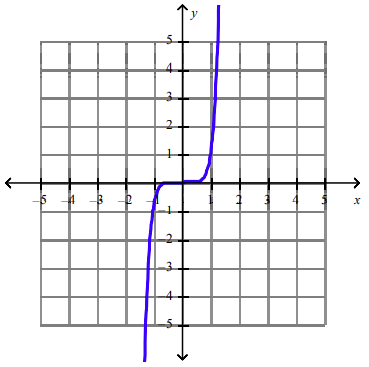 What is the equation of this graph? | back 113 y = x7 |
front 114 The relationship between the Fahrenheit and Celsius temperature scales is given by the linear function. F = 9/5 C + 32 What is the F-intercept and what does it represent? | back 114 32, Fahrenheit temperature corresponding to 0°C |
front 115 Classify the function as a Polynomial function, a Rational function, an algebraic function, or other. f(x) = -8x-7 - x-5 - 7 Select the correct answer. | back 115 c |
front 116  Use the table to evaluate the expression (f ⚬ g)(6). | back 116 2 |
front 117  | back 117 f(x) |
front 118 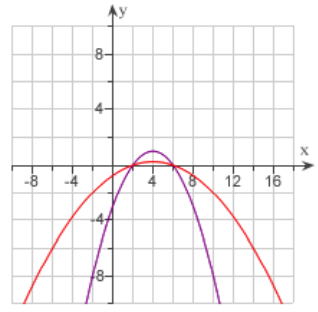 Which of the following is the equation for the function g(x)? Select
the correct answer. | back 118 d |
front 119 The graph of the function f(x) = x2 - 11x + 7 has been stretched horizontally by a factor of 2. Find the function for the transformed graph. | back 119 g(x) = x2-22x+28/4 |
front 120 Plot the graph of the function f in an appropriate viewing window. f(x) = x3/x3+5 | back 120 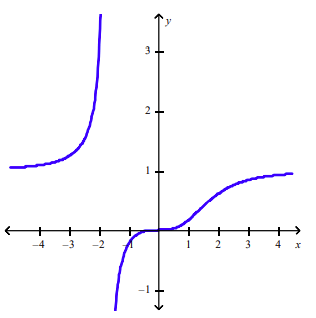 |
front 121 Plot the graph of the function f in an appropriate viewing window. f(x) = x + 0.05sin50x | back 121 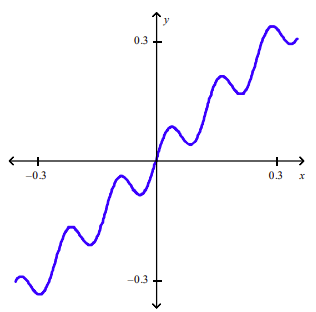 |
front 122 Starting with the graph of y = ex, find the equation of
the graph that results from reflecting about the line y = 1. Select
the correct answer. | back 122 d |
front 123 Use the Law of Exponents to rewrite and simplify the expression. x4nx5n+1/xn-3 | back 123 x8n + 4 |
front 124 If a bacteria population starts with 100 bacteria and doubles every three hours, then the number of bacteria after t hours is n = f(t) = 100(2t/3) When will the population reach 55,000? Round the answer to the
nearest tenth. | back 124 b |
front 125 Find f-1(a) for the function f and the real number a.
Select the correct answer. | back 125 b |
front 126 Find the exact value of the given expression. sin-1 1/2 | back 126 π/6 |
front 127 Use the laws of logarithms to expand the expression. ln(x+4/x-5)1/2 | back 127 1/2 ln (x + 4) - 1/2 ln (x - 5) |
front 128 Simplify the expression. Select the correct answer. e2ln5 a. 25 | back 128 a |
front 129 If f(x) = x2 - x + 6, evaluate the difference quotient f(a+h)-f(a)/h. | back 129 none of these |
front 130 A rectangle has perimeter 12m. Express the area of the rectangle as a
function A(l) of the length l of one of its sides. Select the correct
answer. | back 130 c |
front 131 Find the domain of the function f(x) = x/-5sinx+7 | back 131 (-∞, ∞) |
front 132 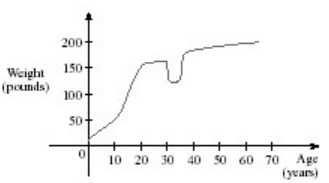 The graph shown gives the weight of a certain person as a function of
age. Find the age at which the person started an exercise program.
Select the correct answer. | back 132 d |
front 133 An open rectangular box with volume 6m3 has a square base. Express the surface area of the box as a function S(x) of the length x of a side of the base. | back 133 S(x) = x2 + 24/x |
front 134 Determine whether f is even, odd, or neither. Select the correct answer. f(x) = 6x2/x4+3 a. neither | back 134 b |
front 135 Find the range of the function. y = 4 + cos x | back 135 [3,5] |
front 136 If f(x) = x + 5 and h(x) = 4x - 10, find a function g such that g ⚬ f = h. | back 136 g(x) = 4x - 30 |
front 137 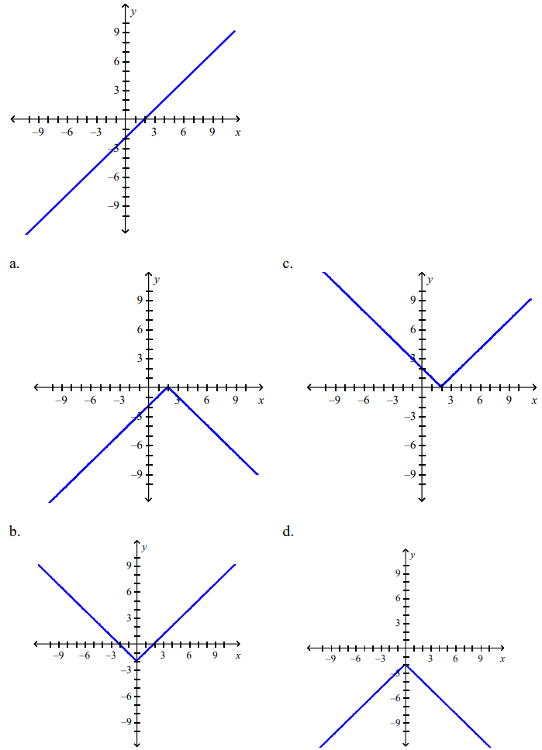 The graph of the function follows. Choose the graph of y = |f(x)| | back 137 c |
front 138 Suppose that the graph of is given f is given. Describe how the graph of the function y = f(x - 3) - 3 can be obtained from the graph of f. Select the correct answer. a. Shift the graph 3 units to the right and 3 units down. | back 138 a |
front 139 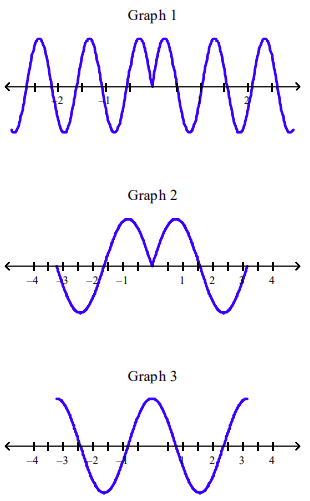 Which of the following graphs is the graph of the function? f(x) = sin|2x| | back 139 graph 2 |
front 140 Plot the graph of the function f in an appropriate viewing window. f(x) = x4/x4+2 | back 140 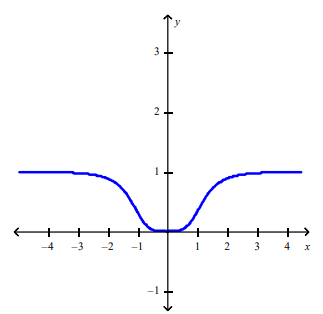 |
front 141 Find the points of intersection of the graphs of the functions. Express your answers accurate to five decimal places. Select the correct answer. f (x) = 0.5x3 – 1.8x2 + 2.2x – 4; g(x) = 2.8x – 4.3 a. (–0.55126, –5.84352), | back 141 d |
front 142 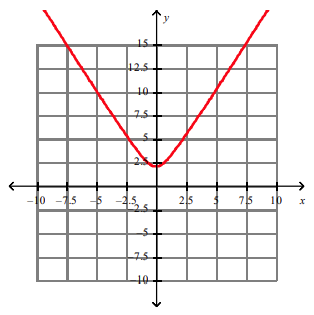 The function f(x) = √4+cx2 is graphed below. | back 142 c > 0 |
front 143 Find the inverse function of f(x) = x+1/3x+1 | back 143 f-1(x) = - x-1/3x-1 |
front 144 Determine whether the function is one-to-one. f(x) = √4-x2 a. Yes | back 144 b |
front 145 Find the exact value of the given expression. tan-1 1 | back 145 π/4 |
front 146 Use the laws of logarithms to expand the expression. ln(x+5/x-6)1/2 | back 146 1/2ln(x + 5) - 1/2ln(x - 6) |
front 147 Simplify the expression. Select the correct answer. e3ln6 a. 9 | back 147 c |
front 148 Solve the equation 4ex + 5 = 2 | back 148 x = ln 1/2 - 5 |
front 149 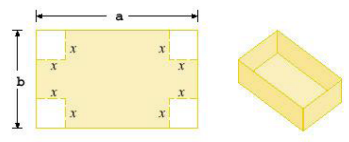 A box with an open top is to be constructed from a rectangular piece of card board with dimensions b = 4 in. by a = 28 in. by cutting out equal squares of side at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. | back 149 V(x) = 4x4 -64x2 + 112x |
front 150 Find an expression for the function y = f(x) whose graph is the
bottom half of the parabola x + (6 - y)2 = 0. Select the
correct answer. | back 150 a |
front 151 Find the domain of the function. f(x) = 7x+1/x2 | back 151 (-∞,0)∪(0,∞) |
front 152 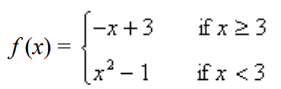 Find the domain and sketch the graph of the function. What is its range? | back 152 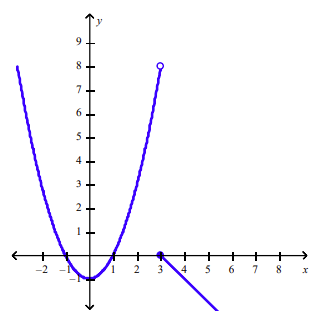 D: (-∞,∞) |
front 153 Find the domain. Select the correct answer. g(u) = √u - √3-u a. (0,3) | back 153 d |
front 154 Graph the function by hand, not by plotting points, but by starting with the graph of one of the standard functions and then applying the appropriate transformations. y = 4 + 2x - x2 | back 154 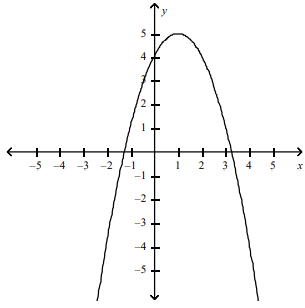 |
front 155 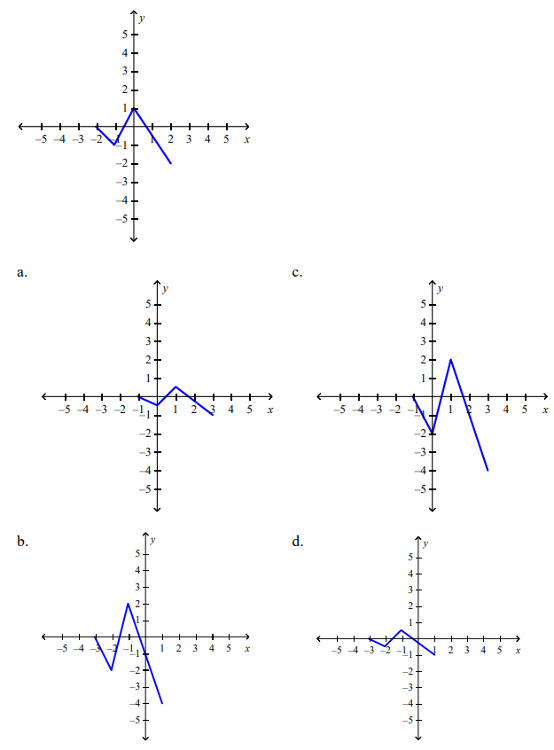 The graph of the function follows. Choose the graph of y = 1/2f(x - 1) | back 155 a |
front 156 Sketch the graph of y = -1-cosx over one period. | back 156 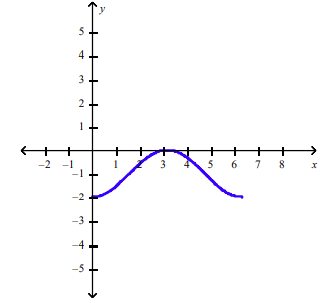 |
front 157 Find the function f ⚬ g and its domain if f(x) = x-1/x and g(x) = x/x+3. | back 157 -3/x D = (-∞,-3)∪(-3,0)∪(0,∞) |
front 158 The graph of the function f(x) = x2 - 11x + 7 has been
stretched horizontally by a factor of 2. Find the function for the
transformed graph. Select the correct answer. | back 158 c |