Instructions for Side by Side Printing
- Print the notecards
- Fold each page in half along the solid vertical line
- Cut out the notecards by cutting along each horizontal dotted line
- Optional: Glue, tape or staple the ends of each notecard together
UCF CAP 6721 Ray Tracing Test 1
front 1 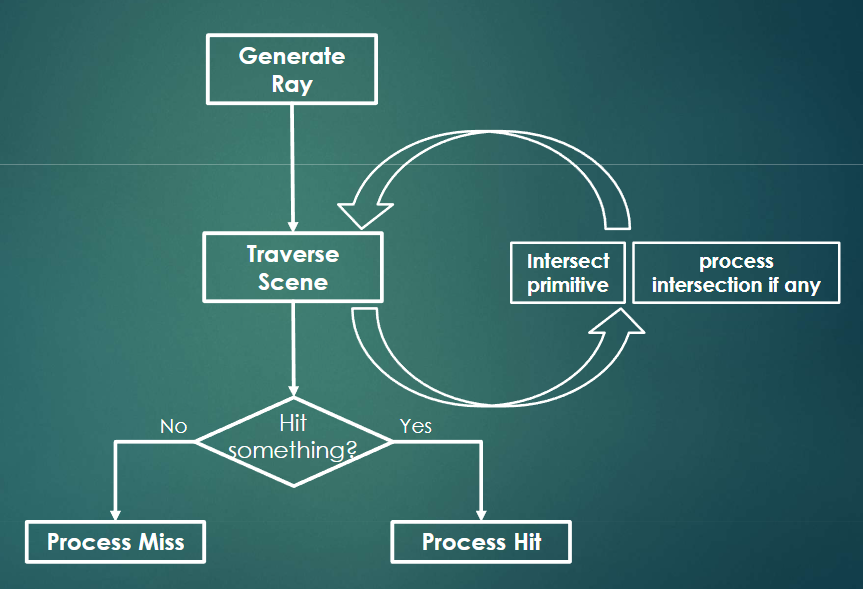 understand this roughly | back 1 understand this roughly |
front 2 Right handed or left handed coord system | back 2 Lay hand flat along x axis curl fingers to y then which ever thumb points in the direction of z is the handedness |
front 3 Vectors only consist of what? | back 3 Direction and magnitude where magnitude is length |
front 4 How to generate a vector between two points? | back 4 Remember it as destination minus source, if we held a rubber band at a destination and pulled it to the source it would snap to destination and that's the direction of the vector. |
front 5 How to do dot product of two vectors u and v, and what does it do? | back 5 u dot v = xu*xv + yu*yv + zu*zv, notice! this produces a scaler value not another vector The equation is equal to ||u|| ||v|| cos(θ) when the angle is 0 meaning the vectors are overlapping cos(0) is 1, think unit vector, if the angle is 90 the cos(90) produces 0. the closer to 1 the more they overlap. If the magnitudes are 1 and the angle is small we can get an equivalent dot product to two vectors with almost 90 degrees if the magnitudes are large. |
front 6 what happens when you dot a vector with itself | back 6 you get the distance squared, so if you need its length/magnitude dot it with itself then square root it |