Print Options

Card layout: ?

← Back to notecard set|Easy Notecards home page

Instructions for Side by Side Printing
  1. Print the notecards
  2. Fold each page in half along the solid vertical line
  3. Cut out the notecards by cutting along each horizontal dotted line
  4. Optional: Glue, tape or staple the ends of each notecard together
  1. Verify Front of pages is selected for Viewing and print the front of the notecards
  2. Select Back of pages for Viewing and print the back of the notecards
    NOTE: Since the back of the pages are printed in reverse order (last page is printed first), keep the pages in the same order as they were after Step 1. Also, be sure to feed the pages in the same direction as you did in Step 1.
  3. Cut out the notecards by cutting along each horizontal and vertical dotted line
To print: Ctrl+PPrint as a list

6 notecards = 2 pages (4 cards per page)

Viewing:

Calc 2

front 1

Ratio Test:

When does it converge & diverge & is inconclusive.

back 1

if the lim n-> ∞ < 1 then the series converges

if the lim n-> ∞ < 1 then the series Diverges

if the lim n-> ∞ == 1 then the series is inconclusive

front 2

P - Series:

When does a series converge, and diverge.

back 2

The Series converges if P> 1, diverges if P <= 1.

front 3

Divergence Test:

When does it converge & diverge & is inconclusive.

back 3

of the lim n-> 0, then the test is inconclusive.

front 4

Direct Comparison Test:

When does a series converge, and diverge.

back 4

  • If 0≤an≤bn (bn converges then an also converges)
  • If an≥bn≥0 (if bn diverges then an also diverges)

front 5

Limit Comparison Test:

What is the formula for the test?

What does L have to be to converge?

What does L have to be to diverge?

back 5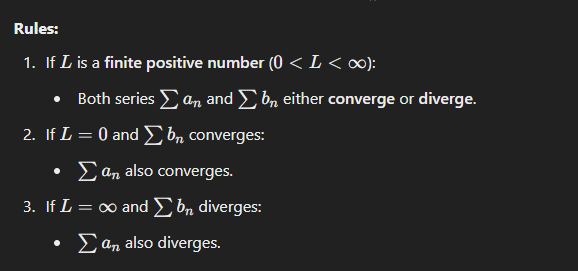

If L is a finite positive number (0 < L < ∞)

Both series (an) and (bn) either converge or diverge)

If L = 0 and Bn converges

An also converges

if L = ∞ and Bn Diverges

then An also diverges

front 6

Alternating Series Test:

When does it converge, and diverge?

back 6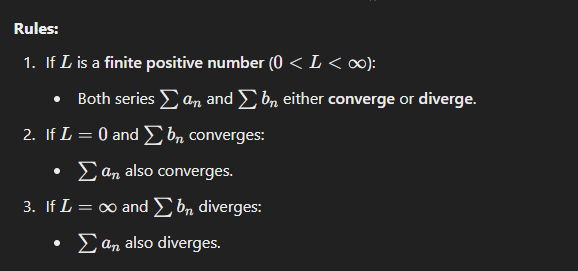

When Lim n->oo an = 0