A manufacturer claims that its compact fluorescent bulbs contain an average of 1.2 mg of mercury.

State the hypotheses for a two-tailed test, using the manufacturer’s claim about the mean as the null hypothesis.

H ₀: μ = 1.2 mg vs. H ₁: μ ≠ 1.2 mg

A survey of 4,581 U.S. households that owned a mobile phone found that 58 percent are satisfied with the coverage of their cellular phone provider. Assuming that this was a random sample, construct a 90% confidence interval for the true proportion of satisfied U.S. mobile phone owners. (Round your answers to 3 decimal places.)

p±z√(p(1-p)/n)

.58±1.645√(.58(.42)/4581)

= .58±.0120 = (.568, .592)

The process that produces Sonora Bars (a type of candy) is intended to produce bars with a mean weight of 56 gm. The process standard deviation is known to be 0.77 gm. A random sample of 49 candy bars yields a mean weight of 55.82 gm. Find the p-value for a test to see whether the candy bars are smaller than they are supposed to be.

a) Between .05 and .10
b) Less than .01
c) Between .01 and .025
d) Between .025 and .05

a) Between .05 and .10

z _calc = (55.82 − 56)/[(0.77)/49^1/2] = −1.63636

and z _.05 = −1.645,

or find the exact p-value as =NORM.S.DIST(-1.63636,1) = .0509.

Construct a confidence interval for μ assuming that each sample is from a normal population.

(a) x¯x¯ = 30, σ = 5, n = 13, 90 percentage confidence. (Round your answers to 2 decimal places.)

(b) x¯x¯ = 124, σ = 10, n = 27, 99 percentage confidence. (Round your answers to 2 decimal places.)

(c) x¯x¯ = 12.1, σ = 1.1, n = 50, 95 percentage confidence. (Round your answers to 3 decimal places.)

a) 30 ± 1.645(5/√13) = 30 ± 2.28
or (27.72, 32.28)

b) 124 ± 2.576(10/√27) = 124 ± 4.96
or (119.04, 128.96)

c) 12.1 ± 1.96(1.1/√50) = 12.1 ± .305
or (11.795, 12.405)

In a recent survey, 10 percent of the participants rated Pepsi as being "concerned with my health." PepsiCo's response included a new "Smart Spot" symbol on its products that meet certain nutrition criteria, to help consumers who seek more healthful eating options.

Suppose a follow-up survey shows that 28 of 200 persons now rate Pepsi as being "concerned with my health."

Calculate the z statistic. (Round your answer to 3 decimal places.)

At α = .05, would a follow-up survey showing that 28 of 200 persons now rate Pepsi as being “concerned with my health” provide sufficient evidence that the percentage has increased?

a) H ₀: π ≤ .10 vs. H ₁: π > .10.

z= (.1400-.10)/√(.10(.90)/200)

z = 1.886

b) Yes

p-value = 1 – NORM.S.DIST(1.886,1) = 1 – .9704 = .0296 and .0296 < .05, so reject H ₀ and conclude that the proportion who believe Pepsi is concerned with consumers’ health has increased.

The average age of a part-time seasonal employee at a Vail Resorts ski mountain has historically been 37 years.

State the hypotheses one would use to test if this average has decreased since the last season.

a) H ₀: μ ≥ 37 yrs vs. H ₁: μ < 37 yrs

b) H ₀: μ ≤ 37 yrs vs. H ₁: μ > 37 yrs

c) H ₀: μ = 37 yrs vs. H ₁: μ ≠ 37 yrs

a) H₀: μ ≥ 37 yrs vs. H₁: μ < 37 yrs

In a two-tailed test, a statistician got a z test statistic of 1.82. What is the p-value?

a) .0708
b) .0688
c) .0301
d) .0874

b) .0688

From Appendix C we get 2 × P(Z > 1.82) = 2 × .0344 = .0688. The Excel version of this calculation is =2*(1-NORM.S.DIST(1.82,1)) = 0.0688.

In the nation of Gondor, the EPA requires that half the new cars sold will meet a certain particulate emission standard a year later. A sample of 64 one-year-old cars revealed that only 24 met the particulate emission standard. The test statistic to see whether the proportion is below the requirement is

a) -1.645
b) -2.000
c) -1.960
d) -2.066

b) -2.000

p = 24/64 = .375, π ₀ = .50, z _calc = (.375 − .50)/[(.50)(1 − .50)/64]^1/2 = −2.000.

(a) A poll of 2,237 likely voters was conducted on the president’s performance. Approximately what margin of error would the approval rating estimate have if the confidence level is 95%? (Round your answer to 4 decimal places.)

(b) The poll showed that 46 percent approved the president’s performance. Construct a 90 percent confidence interval for the true proportion. (Round your answers to 4 decimal places.)

(c) Would you agree that the percentage of all voters opposed is likely to be 50 percent?

a) .0210

Margin of error = 1.960 √(.50(1-.5)/2237)

= .0207

b) (.4425, .4775)

p±z√(p(1−p)/n)

=0.46±1.645√(0.46(1 −0.46)/2,237)

=0.46±0.0173   or (0.4427, 0.4773)

c) No, the confidence interval does not contain .50.

Last year, 10 percent of all teenagers purchased a new iPhone. This year, a sample of 260 randomly chosen teenagers showed that 39 had purchased a new iPhone. To test whether the percentage has risen, the p-value is approximately

a) .0501
b) .0314
c) .0492
d) .0036

d) .0036

p = 39/260 = .15, π ₀ = .10, z _calc = (.15 − .10)/[(.10)(1 − .10)/260]^1/2 = 2.68742. From Appendix C we get P(Z > 2.69) = .0036, or from Excel =1-NORM.S.DIST(2.68742,1) = .0036.

The process that produces Sonora Bars (a type of candy) is intended to produce bars with a mean weight of 56 gm. The process standard deviation is known to be 0.77 gm. A random sample of 49 candy bars yields a mean weight of 55.82 gm. Find the test statistic to see whether the candy bars are smaller than they are supposed to be.

a) -1.677
b) -1.645
c) -1.636

c) -1.636

z _calc = (55.82 − 56)/[(0.77)/49^1/2] = −1.63636.

In a sample of 679 new websites registered on the Internet, 42 were anonymous (i.e., they shielded their name and contact information).

(a) Construct a 95 percent confidence interval for the proportion of all new websites that were anonymous. (Round your answers to 4 decimal places.)

(b) May normality of p be assumed?

a) (.0437, .0800)

p = 42/679 = .06186

p±z√(p(1-p)/n)

.06186 ± 1.960 √.06186(1-.06186)/679)

= .06186 ± .0181 or (.0437, .0800)

b) Yes

A random sample of 150 items is drawn from a population whose standard deviation is known to be σ = 40. The sample mean is x¯ = 790.

(a) Construct an interval estimate for μ with 99 percent confidence. (Round your answers to 1 decimal place.)

(b) Construct an interval estimate for μ with 99 percent confidence, assuming that σ = 80. (Round your answers to 1 decimal place.)

(c) Construct an interval estimate for μ with 99 percent confidence, assuming that σ = 160. (Round your answers to 1 decimal place.)

(d) Describe how the confidence interval changes as σ increases.

a) (781.6, 798.4)

790 ± 2.58 (40/√150)

b) (773.2, 806.8)

790 ± 2.58 (80/√150)

c) (756.3, 823.7)

790 ± 2.58 (160/√150)

d) The confidence interval gets wider as σ increases.

A firm decides to test its employees for illegal drugs.

(a) State the null and alternative hypotheses.

(b) Define Type I and II errors.

(c) In this case, which type of error has the more severe consequences?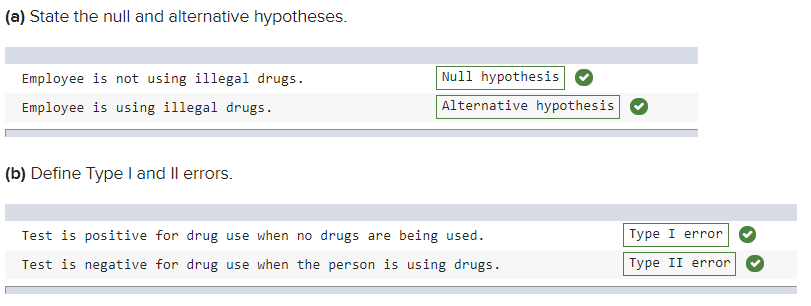

a&b in image attachment

c) Type II error

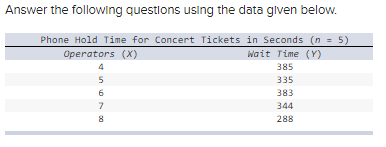A) Choose the correct set of hypotheses for a two-tailed test for a zero slope.

a) H ₀: β ₁ ≥ 0 vs. H ₁: β ₁ < 0

b) H ₀: β ₁ ≤ 0 vs. H ₁: β ₁ > 0

c) H ₀: β ₁ = 0 vs. H ₁: β ₁ ≠ 0

B-1) What is the p-value? (Round your answer to 4 decimal places.)

B-2) State the 95% confidence interval for the slope.

C) Choose the correct statement.

-The slope is not significantly different from zero.

-The slope is significantly different from zero.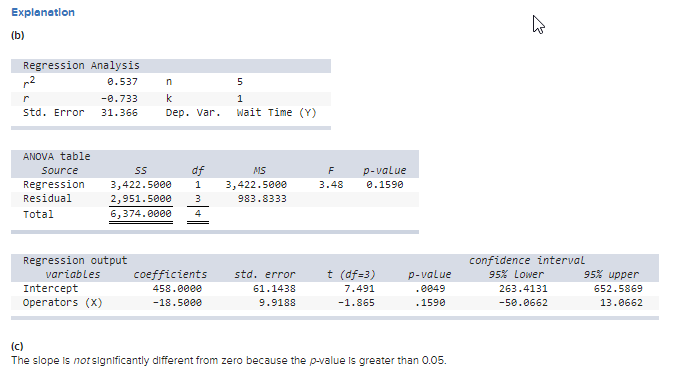

A) c) H ₀: β ₁ = 0 vs. H ₁: β ₁ ≠ 0

B-1) .1590

B-2) The confidence interval is from -50.0662 to 13.0662

C) The slope is not significantly different from zero.

The fitted regression is Sales = 902-32.8(Price)

A-1) If Price = 1, what is the prediction for Sales? (Round your answer to 1 decimal place.)

A-2) Choose the correct statement.

• An increase in price increases sales.
• A decrease in price decreases sales.
• An increase in price decreases sales.

B) If Price = 22, what is the prediction for Sales? (Round your answer to the nearest whole number.)

C) Choose the right option

• The intercept is not meaningful as a zero price is both unrealistic and unobserved. Correct
• The intercept is meaningful as sales will be maximized when price is zero.

A-1) Sales = 902-1(32.8) = 869.2

A-2) An increase in price decreases sales.

B) Sales = 902 - 22(32.8) = 180

C) The intercept is not meaningful as a zero price is both unrealistic and unobserved.

Use Excel to calculate the sample correlation coefficient for each data set. (Round your answers to 4 decimal places.)

Put each data set into excel and use CORREL(X Data, Y Data)

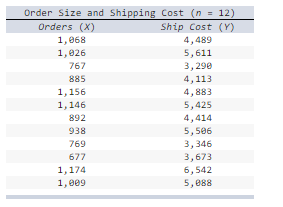A) Choose the right option

• An increase in orders leads to an average decrease in shipping cost.
• An increase in orders leads to an average increase in shipping cost.

B) Choose the correct statement.

• The intercept is not meaningful in this case. Correct
• The intercept is meaningful in this case.

C) Calculate R ². (Round your answer to 4 decimal places.)

D) Interpret the R ². (Round your answer to 4 decimal places.)

A) An increase in orders leads to an average increase in shipping cost.

B) The intercept is not meaningful in this case.

C) .6717

D) 67.17%

The regression equation NetIncome = 2,185 + .0392 Revenue was estimated from a sample of 100 leading world companies (variables are in millions of dollars).

(a-1) Calculate the residual for the x, y pair ($44,681, $3,720). (A negative value should be indicated by a minus sign. Round your answer to 4 decimal places.)

• The regression equation overestimated the net income.
• The regression equation underestimated the net income.

(b-1) Calculate the residual for the x, y pair ($63,662, $4,513). (A negative value should be indicated by a minus sign. Round your answer to 4 decimal places.)

(b-2) Did the regression equation underestimate or overestimate the net income?

• The regression equation overestimated the net income.
• The regression equation underestimated the net income.

a-1)y^= $2,185 + .0392($44,681) = $3,936.4952

ei = 3,720 – 3,936.4952 = –216.4952

a-2) The regression equation overestimated the net income.

b-1) y^ = $2,185 + .0392($63,662) = $4,680.5504

ei = 4,513 – 4,680.5504 = –167.5504

b-2) The regression equation overestimated the net income.

Choose the dependent variable (the response variable to be "explained") and the independent variable (the predictor or explanatory variable).

Dependent Variable

• ELOS
• ALOS

Independent Variable

• ALOS
• ELOS

Obtain the regression equation. (Round your answers to 3 decimal places.)

Calculate R ²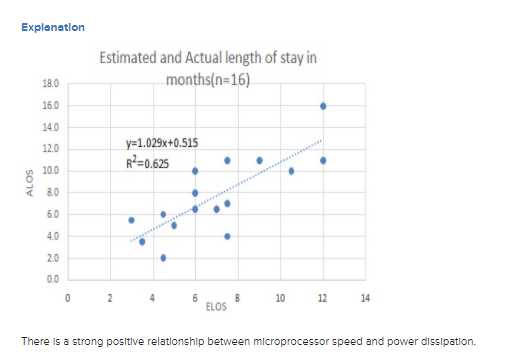

Dependent Variable = ALOS

Independent Variable = ELOS

Regression Equation = Y = 1.029X + .515

R ² = .625

Researchers found a correlation coefficient of r = .50 on personality measures for identical twins. A reporter interpreted this to mean that "the environment orchestrated one-half of their personality differences."

(a) r is a measure of the strength and direction of the linear relationship.

• No
• Yes

(b) r is a measure of the amount of variation.

• Yes
• No

(c) r = 0.5 implies the environment orchestrated one-half of their personality differences.

• True
• False

a) Yes

b) No

c) False

Explanation

No, r measures the strength and direction of the linear relationship, but not the amount of variation explained by the explanatory variable.

Which is not revealed on a scatter plot?

• Nonlinear relationships between X and Y
• Missing data values due to nonresponses
• Pairs of observed (x _i, y_i) data values
• Unusual data values (outliers)

Missing Data values due to nonresponses.

Explanation

Excel simply omits missing data for a scatter plot.

Simple regression was employed to establish the effects of childhood exposure to lead. The effective sample size was about 122 subjects. The independent variable was the level of dentin lead (parts per million). Below are regressions using various dependent variables.

(a) Calculate the t statistic for each slope. From the p-values, which slopes differ from zero at α = .01? (Round your answers to 2 decimal places. Negative values should be indicated by a minus sign.)

(b) It would be inappropriate to assume cause and effect without a better understanding of how the study was conducted.

• No
• Yes

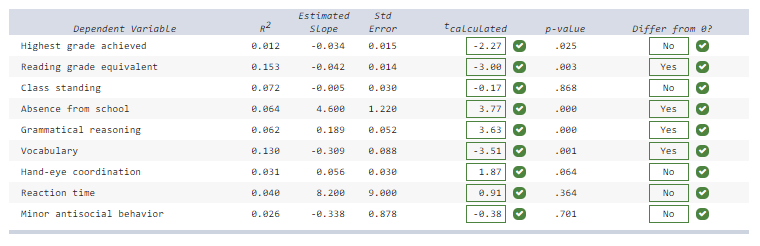
(a) answers in image

t= estimated slope
standard error

(b) Yes